Since the advent of cluster computing over 10 years ago there has been a steady output of new and better direct numerical simulation of homogeneous, isotropic turbulence with spectra and lower-order statistics converging to experiments and many phenomenological models. The next step is to directly compare these simulations to new models and new mathematics, employing the simulated data sets in novel ways, especially when experimental results do not exist or are poorly converged. For example, many of the higher-order moments predicted by the models converge slowly in experiments. The solution with a simulation is to do what an experiment cannot. The calculation and analysis of Yeung, Donzis & Sreenivasan (J. Fluid Mech., this issue, vol. 700, 2012, pp. 5–15) represents the vanguard of new simulations and new numerical analysis that will fill this gap. Where individual higher-order moments of the vorticity squared (the enstrophy) and kinetic energy dissipation might be converging slowly, they have focused upon ratios between different moments that have better convergence properties. This allows them to more fully explore the statistical distributions that eventually must be modelled. This approach is consistent with recent mathematics that focuses upon temporal intermittency rather than spatial intermittency. The principle is that when the flow is nearly singular, during ‘bad’ phases, when global properties can go up and down by many orders of magnitude, if appropriate ratios are taken, convergence rates should improve. Furthermore, in future analysis it might be possible to use these ratios to gain new insights into the intermittency and regularity properties of the underlying equations.

We use data from well-resolved direct numerical simulations at Taylor-scale Reynolds numbers from 140 to 1000 to study the statistics of energy dissipation rate and enstrophy density (i.e. the square of local vorticity). Despite substantial variability in each of these variables, their extreme events not only scale in a similar manner but also progressively tend to occur spatially together as the Reynolds number increases. Though they possess non-Gaussian tails of enormous amplitudes, ratios of some characteristic properties can be closely linked to those of isotropic Gaussian random fields. We present results also on statistics of the pressure Laplacian and conditional mean pressure given both dissipation and enstrophy. At low Reynolds number intense negative pressure fluctuations are preferentially associated with rotation-dominated regions but at high Reynolds number both high dissipation and high enstrophy have similar effects.

The unsteady behaviour in shockwave turbulent boundary layer interaction is investigated by analysing results from a large eddy simulation of a supersonic turbulent boundary layer over a compression–expansion ramp. The interaction leads to a very-low-frequency motion near the foot of the shock, with a characteristic frequency that is three orders of magnitude lower than the typical frequency of the incoming boundary layer. Wall pressure data are first analysed by means of Fourier analysis, highlighting the low-frequency phenomenon in the interaction region. Furthermore, the flow dynamics are analysed by a dynamic mode decomposition which shows the presence of a low-frequency mode associated with the pulsation of the separation bubble and accompanied by a forward–backward motion of the shock.

Turbulent two-phase flows are characterized by the presence of multiple time and length scales. Of particular interest in flows with non-negligible interphase momentum coupling are the time scales associated with interphase turbulent kinetic energy transfer (TKE) and inertial particle dispersion. Point-particle direct numerical simulations (DNS) of homogeneous turbulent flows laden with sub-Kolmogorov size particles report that the time scale associated with the interphase TKE transfer behaves differently with Stokes number than the time scale associated with particle dispersion. Here, the Stokes number is defined as the ratio of the particle momentum response time scale to the Kolmogorov time scale of turbulence. In this study, we propose a two-way coupled stochastic model (CSM), which is a system of two coupled Langevin equations for the fluctuating velocities in each phase. The basis for the model is the Eulerian–Eulerian probability density function formalism for two-phase flows that was established in Pai & Subramaniam (J. Fluid Mech., vol. 628, 2009, pp. 181–228). This new model possesses the unique capability of simultaneously capturing the disparate dependence of the time scales associated with interphase TKE transfer and particle dispersion on Stokes number. This is ascertained by comparing predicted trends of statistics of turbulent kinetic energy and particle dispersion in both phases from CSM, for varying Stokes number and mass loading, with point-particle DNS datasets of homogeneous particle-laden flows.

We consider the two- and three-dimensional spreading of a finite volume of viscous power-law fluid released over a denser inviscid fluid and subject to gravitational and capillary forces. In the case of gravity-driven spreading, with a power-law fluid having strain rate proportional to stress to the power , there are similarity solutions with the extent of the current being proportional to 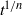in the two-dimensional case and 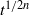in the three-dimensional case. Perturbations from these asymptotic states are shown to retain their initial shape but to decay relatively as 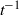in the two-dimensional case and 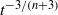in the three-dimensional case. The former is independent of , whereas the latter gives a slower rate of relative decay for fluids that are more shear-thinning. In cases where the layer is subject to a constraining surface tension, we determine the evolution of the layer towards a static state of uniform thickness in which the gravitational and capillary forces balance. The asymptotic form of this convergence is shown to depend strongly on , with rapid finite-time algebraic decay in shear-thickening cases, large-time exponential decay in the Newtonian case and slow large-time algebraic decay in shear-thinning cases.

Harmonic oscillations of the walls of a turbulent plane channel flow are studied by direct numerical simulations to improve our understanding of the physical mechanism for skin-friction drag reduction. The simulations are carried out at constant pressure gradient in order to define an unambiguous inner scaling: in this case, drag reduction manifests itself as an increase of mass flow rate. Energy and enstrophy balances, carried out to emphasize the role of the oscillating spanwise shear layer, show that the viscous dissipation of the mean flow and of the turbulent fluctuations increase with the mass flow rate, and the relative importance of the latter decreases. We then focus on the turbulent enstrophy: through an analysis of the temporal evolution from the beginning of the wall motion, the dominant, oscillation-related term in the turbulent enstrophy is shown to cause the turbulent dissipation to be enhanced in absolute terms, before the slow drift towards the new quasi-equilibrium condition. This mechanism is found to be responsible for the increase in mass flow rate. We finally show that the time-average volume integral of the dominant term is linearly related to the drag reduction.

The swimming trajectories of self-propelled organisms or synthetic devices in a viscous fluid can be altered by hydrodynamic interactions with nearby boundaries. We explore a multipole description of swimming bodies and provide a general framework for studying the fluid-mediated modifications to swimming trajectories. A general axisymmetric swimmer is described as a linear combination of fundamental solutions to the Stokes equations: a Stokeslet dipole, a source dipole, a Stokeslet quadrupole, and a rotlet dipole. The effects of nearby walls or stress-free surfaces on swimming trajectories are described through the contribution of each singularity, and we address the question of how accurately this multipole approach captures the wall effects observed in full numerical solutions of the Stokes equations. The reduced model is used to provide simple but accurate predictions of the wall-induced attraction and pitching dynamics for model Janus particles, ciliated organisms, and bacteria-like polar swimmers. Transitions in attraction and pitching behaviour as functions of body geometry and propulsive mechanism are described. The reduced model may help to explain a number of recent experimental results.

In this work, we investigate the approach of a descending vortex pair to a horizontal ground plane. As in previous studies, the primary vortices exhibit a ‘rebound’, due to the separation of secondary opposite-sign vortices underneath each primary vortex. On each side of the flow, the weaker secondary vortex can become three-dimensionally unstable, as it advects around the stronger primary vortex. It has been suggested in several recent numerical simulations that elliptic instability is the origin of such waviness in the secondary vortices. In the present research, we employ a technique whereby the primary vortices are visualized separately from the secondary vortices; in fact, we are able to mark the secondary vortex separation, often leaving the primary vortices invisible. We find that the vortices are bent as a whole in a Crow-type ‘displacement’ mode, and, by keeping the primary vortices invisible, we are able to see both sides of the flow simultaneously, showing that the instability perturbations on the secondary vortices are antisymmetric. Triggered by previous research on four-vortex aircraft wake flows, we analyse one half of the flow as an unequal-strength counter-rotating pair, noting that it is essential to take into account the angular velocity of the weak vortex around the stronger primary vortex in the analysis. In contrast with previous results for the vortex–ground interaction, we find that the measured secondary vortex wavelength corresponds well with the displacement bending mode, similar to the Crow-type instability. We have analysed the elliptic instability modes, by employing the approximate dispersion relation of Le Dizés & Laporte (J. Fluid Mech., vol. 471, 2002, p. 169) in our problem, finding that the experimental wavelength is distinctly longer than predicted for the higher-order elliptic modes. Finally, we observe that the secondary vortices deform into a distinct waviness along their lengths, and this places two rows of highly stretched vertical segments of the vortices in between the horizontal primary vortices. The two rows of alternating-sign vortices translate towards each other and ultimately merge into a single vortex row. A simple point vortex row model is able to predict trajectories of such vortex rows, and the net result of the model’s ‘orbital’ or ‘passing’ modes is to bring like-sign vortices, from each secondary vortex row, close to each other, such that merging may ensue in the experiments.

A statistical closure is proposed for a Galerkin model of an incompressible periodic cylinder wake. This closure employs Jaynes’ maximum entropy principle to infer the probability distribution for mode amplitudes using exact statistical balance equations as side constraints. The analysis predicts mean amplitude values and modal energy levels in good agreement with direct Navier–Stokes simulation. In addition, it provides an analytical equation for the modal energy distribution.

We present an analytical model that describes the linear interaction of two successive shocks launched into a non-uniform density field. The re-shock problem is important in different fields, inertial confinement fusion among them, where several shocks are needed to compress the non-uniform target. At first, we present a linear theory model that studies the interaction of two successive shocks with a single-mode density perturbation field ahead of the first shock. The second shock is launched after the sonic waves emitted by the first shock wave have vanished. Therefore, in the case considered in this work, the second shock only interacts with the entropic and vortical perturbations left by the first shock front. The velocity, vorticity and density fields are later obtained in the space behind the second shock. With the results of the single-mode theory, the interaction with a full spectrum of random-isotropic density perturbations is considered by decomposing it into Fourier modes. The model describes in detail how the second shock wave modifies the turbulent field generated by the first shock wave. Averages of the downstream quantities (kinetic energy, vorticity, acoustic flux and density) are easily obtained either for two-dimensional or three-dimensional upstream isotropic spectra. The asymptotic limits of very strong shocks are discussed. The study shown here is an extension of previous works, where the interaction of a planar shock wave with random isotropic vorticity/entropy/acoustic spectra were studied independently. It is also a preliminary step towards the understanding of the re-shock of a fully turbulent flow, where all three of the modes, vortical, entropic and acoustic, might be present.

This paper numerically investigates the effects of a harmonic volume forcing of prescribed frequency on the turbulent pipe flow at a Reynolds number, based on bulk velocity and pipe diameter, of 5900. The thickness of the Stokes layer, resulting from the oscillatory flow component, is a small fraction of the pipe radius and therefore the associated vorticity is confined within a few wall units. 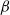The harmonic forcing term is prescribed so that the ratio of the oscillating to the mean bulk velocity () ranges between 1 and 10.6. In all cases the oscillatory flow obeys the Stokes analytical velocity distribution while remarkable changes in the current component are observed. At intermediate values 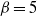, a relaminarization process occurs, while for 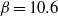, turbulence is affected so much by the harmonic forcing that the near-wall coherent structures, although not fully suppressed, are substantially weakened. The present study focuses on the analysis of the time- and space-averaged statistics of the first- and second-order moments, vorticity fluctuations and Reynolds stress budgets. Since the flow is unsteady not only locally but also in its space-averaged dynamics, it can be analysed using phase-averaged and time-averaged statistics. While the former gives information about the statistics of the fluctuations about the mean, the latter, postponed to a subsequent paper, shows how the mean is affected by the fluctuations. Clearly, the two phenomena are connected and both of them deserve investigation.

Since Trösch (Proceedings of the 4th International Conference on Applied Numerical Modeling, Tainan, Taiwan, 1984 (ed. H. M. Hsia, Y. L. Chou, S. Y. Wang & S. J. Hsieh) Science and Technology Series, vol. 63, 1986, pp. 307–311. American Astronautical Society) found trapped sub-inertial oscillations in computations of low-frequency variability in the Lake of Lugano, models of trapping have generally considered evenly spaced isobaths parallel to shorelines with approximate boundary conditions at any shelf–ocean boundary. Here an asymptotic analysis for slowly varying topography and accurate spectral computations demonstrate trapping on non-rectilinear shelves. It is shown that changes in any of three factors, isobath curvature, distance from the coast and the shelf-break, and the slope at the shelf-break, are sufficient on their own to give trapping. Continental shelves that abut smoothly onto the open ocean are considered thus avoiding the shelf–ocean boundary condition approximation and allowing the accuracy of previous approximations to be assessed.

Nonlinear responses of surface waves in rigid square and nearly square tanks partially filled with liquid subjected to obliquely horizontal, sinusoidal excitation are investigated theoretically and experimentally. Two predominant modes of sloshing are significantly coupled nonlinearly because their natural frequencies are nearly identical resulting in 1:1 internal resonance. Therefore, if only one of these modes is directly excited, the other mode is indirectly excited due to the nonlinear coupling. In the nonlinear theoretical analysis, the modal equations of motion are derived for the two predominant sloshing modes as well as five higher sloshing modes. The linear viscous terms are incorporated in order to consider the damping effect of sloshing. The expressions for the frequency response curves are determined using van der Pol’s method. The influences of the excitation direction and the aspect ratio of the tank cross-section on the frequency response curves are numerically examined. Planar and swirl motions of sloshing, and Hopf bifurcations followed by amplitude modulated motions including chaotic motions, are predicted when the excitation frequency is close to one of the natural frequencies of the two predominant sloshing modes. Lyapunov exponents are calculated and reveal the excitation frequency range over which liquid chaotic motions occur. In addition, bifurcation sets are shown to clarify the influences of the parameters on the change in the structural stability. The theoretically predicted results are in good agreement with the measured data, thus the theoretical analysis was experimentally validated.

Numerical simulations with single-step chemistry and detailed transport are used to study premixed hydrogen/air flames in two-dimensional channel-like domains with periodic boundary conditions along the horizontal boundaries as a function of the domain height. Both unity Lewis number, where only hydrodynamic instability appears, and subunity Lewis number, where the flame propagation is strongly affected by the combined effect of hydrodynamic and thermodiffusive instabilities are considered. The simulations aim at studying the initial linear growth of perturbations superimposed on the planar flame front as well as the long-term nonlinear evolution. The dispersion relation between the growth rate and the wavelength of the perturbation characterizing the linear regime is extracted from the simulations and compared with linear stability theory. The dynamics observed during the nonlinear evolution depend strongly on the domain size and on the Lewis number. As predicted by the theory, unity Lewis number flames are found to form a single cusp structure which propagates unchanged with constant speed. The long-term dynamics of the subunity Lewis number flames include steady cell propagation, lateral flame movement, oscillations and regular as well as chaotic cell splitting and merging.

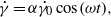Viscoelastic properties of complex fluids are usually extracted by applying an oscillatory shear rate ( where 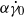is a constant which is small for a linear response to make sense) to the fluid. This leads to a complex effective viscosity where its real part carries information on viscous effects while its imaginary part informs us on elastic properties. We show here theoretically, by taking a dilute vesicle suspension as an example, that application of a pure shearing oscillation misses several interesting microscopic features of the suspension. It is shown that if, in addition to the oscillatory part, a basic constant shear rate is applied to the suspension (so that the total shear rate is 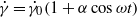, with 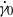a constant), then the complex viscosity reveals much more insightful properties of the suspension. First, it is found that the complex viscosity exhibits a resonance for tank-treading vesicles as a function of the frequency of oscillation. This resonance is linked to the fact that vesicles, while being in the stable tank-treading regime (with their main axis having a steady orientation with respect to the flow direction), possess damped oscillatory modes. Second, in the region of parameter space where the vesicle exhibits either vacillating-breathing (permanent oscillations of the main axis about the flow direction and breathing of the shape) or tumbling modes, the complex viscosity shows an infinite number of resonances as a function of the frequency. It is shown that these behaviours markedly differ from that obtained when only the classical oscillation 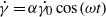is applied. The results are obtained numerically by solution of the analytical constitutive equation of a dilute vesicle suspension and confirmed analytically by a linear-response phenomenological theory. It is argued that the same type of behaviour is expected for any suspension of soft entities (capsules, red blood cells, etc.) that exhibit periodic motion under constant shear flow. We shall also discuss the reason why this type of behaviour could not have been captured by existing constitutive laws of complex fluids.

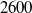Experiments on a circular starting jet generated by a piston–cylinder arrangement, over a range of Reynolds number from to 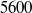, are conducted so as to investigate the development of the trailing shear layer during the leading vortex ring formation, as well as the corresponding effects on the pinch-off process. Results obtained by digital particle image velocimetry (DPIV) show that secondary vortices start to develop in the trailing jet only after the critical time scale, the ‘formation number’, is achieved. The subsequent growth of the secondary vortices reduces the vorticity flux being fed into the leading vortex ring and, as a consequence, constrains the growth of leading vortex ring with larger circulation. Evolution of perturbation waves into secondary vortices is found to associate with growth and translation of the leading vortex ring during the formation process. A dimensionless parameter ‘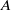’, defined as 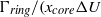), is therefore proposed to characterize the effect of the leading vortex ring on suppressing the nonlinear development of instability in the trailing shear layer, i.e. the initial roll-up of the secondary vortices. In a starting jet, 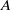follows a decreasing trend with the formation time 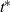. A critical value 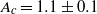is identified experimentally, which physically coincides with the initiation of the first secondary vortex roll-up and, therefore, indicates the onset of pinch-off process.

Flow control with the goal of reducing the skin-friction drag on the fluid–solid interface is an active fundamental research area, motivated by its potential for significant energy savings and reduced emissions in the transport sector. Customarily, the performance of drag reduction techniques in internal flows is evaluated under two alternative flow conditions, i.e. at constant mass flow rate or constant pressure gradient. Successful control leads to reduction of drag and pumping power within the former approach, whereas the latter leads to an increase of the mass flow rate and pumping power. In practical applications, however, money and time define the flow control challenge: a compromise between the energy expenditure (money) and the corresponding convenience (flow rate) achieved with that amount of energy has to be reached so as to accomplish a goal which in general depends on the specific application. Based on this idea, we derive two dimensionless parameters which quantify the total energy consumption and the required time (convenience) for transporting a given volume of fluid through a given duct. Performances of existing drag-reduction strategies as well as the influence of wall roughness are re-evaluated within the present framework; how to achieve the (application-dependent) optimum balance between energy consumption and convenience is addressed. It is also shown that these considerations can be extended to external flows.

A two-dimensional model for the analysis of sloshing phenomena in shallow-water conditions has been defined using Boussinesq-type depth-averaged equations. Thanks to a modal decomposition of the spatial field, the present model allows a straightforward and simple treatment of the exciting forces and can describe a generic motion. Comparisons with the experimental data available in the literature and with a smoothed particle hydrodynamics (SPH) scheme proved the proposed shallow-water model to be accurate, fast and robust.

We revisit the classic problem of the stability of drops and jets held by surface tension, while regarding the compressibility of bulk fluids and spatial dimensions as free parameters. By mode analysis, it is shown that there exists a critical compressibility above which the drops (and discs) become unstable for a spherical perturbation. For a given value of compressibility (and of the surface tension and the density at equilibrium), this instability criterion provides a minimal radius below which the drop cannot be in stable equilibrium. According to the existence of the above unstable mode of the drop, which corresponds to a homogeneous perturbation of a cylindrical jet, the dispersion relation of Rayleigh–Plateau instability for cylinders drastically changes. In particular, we identify another critical compressibility above which the homogeneous unstable mode is predominant. The analysis is carried out for non-relativistic and relativistic perfect fluids, the self-gravity of which is ignored.

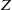The first generation of stars had very different properties than later stellar generations, as they formed from a ‘pristine’ gas that was completely free of heavy elements. Normal star formation took place only after the first stars had polluted the surrounding turbulent interstellar gas, increasing its local heavy-element mass concentration, , beyond a ‘critical’ threshold value, 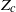(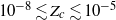). Motivated by this astrophysical problem, we investigate the fundamental physics of the pollution of pristine fluid elements in statistically homogeneous and isotropic compressible turbulence. Turbulence stretches the pollutants, produces concentration structures at small scales, and brings the pollutants and the unpolluted flow in closer contact. The pristine material is polluted when exposed to the pollutant sources or the fluid elements polluted by previous mixing events. Our theoretical approach employs the probability distribution function (p.d.f.) method for turbulent mixing, as the fraction of pristine mass corresponds to the low tail of the density-weighted concentration p.d.f. We adopt a number of p.d.f. closure models and derive evolution equations for the pristine fraction from the models. To test and constrain the prediction of theoretical models, we conduct numerical simulations for decaying passive scalars in isothermal turbulent flows with Mach numbers of 0.9 and 6.2, and compute the mass fraction, 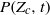, of the flow with 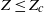. In the Mach 0.9 flow, the evolution of 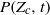is well-described by a continuous convolution model and goes as 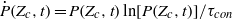, if the mass fraction of the polluted flow is larger than 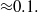If the initial pollutant fraction is smaller than 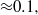an early phase exists during which the pristine fraction follows an equation derived from a nonlinear integral model: 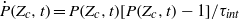. The time scales 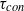and 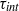are measured from our simulations. When normalized to the flow dynamical time, the decay of 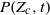in the Mach 6.2 flow is slower than at Mach 0.9 because the time scale for scalar variance decay is slightly larger and the low tail of the concentration p.d.f. broadens with increasing Mach number. We show that 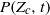in the Mach 6.2 flow can be well fitted using a formula from a generalized version of the self-convolution model.