In this work, we report the first experimental observation of electrically driven Moffatt vortices between conical surfaces. The flow field is captured using a synchronized multi-camera particle image velocimetry experiment. The results reveal a flow bifurcation resembling Moffatt vortices in canola oil with −12 kV applied to an axisymmetric point-to-plane electrode set-up. The formation of such vortices was predicted theoretically; however, to the best of our knowledge, experimental observations were not reported earlier. The experimental results of the present work are shown to be in agreement with the available theoretical predictions. In addition, the observed vortices are slightly transient, suggesting the next bifurcation reminiscent of the Taylor vortices in the Taylor–Couette flow.

We investigate the development of three-dimensional instabilities on a time-dependent round jet undergoing the axisymmetric Kelvin–Helmholtz (KH) instability. A non-modal linear stability analysis of the resulting unsteady roll-up into a vortex ring is performed based on a direct-adjoint approach. Varying the azimuthal wavenumber $m$, the Reynolds number ${Re}$ and the aspect ratio $\alpha$ of the jet base flow, we explore the potential for secondary energy growth beyond the initial phase when the base flow is still quasi-parallel and universal shear-induced transient growth occurs. For ${Re}=1000$ and $\alpha = 10$, the helical $m=1$ and double-helix $m=2$ perturbations stand as global optimals with larger growth rates in the post roll-up phase. The secondary energy growth stems from the development of elliptical (E-type) and hyperbolic (H-type) instabilities. For $m>2$, the maximum of the kinetic energy of the optimal perturbation moves from the large scale vortex core towards the thin vorticity braid. With a Reynolds number one order of magnitude larger, the kinetic energy of the optimal perturbations exhibits sustained growth well after the saturation time of the base flow KH wave and the underlying length scale selection favours higher azimuthal wavenumbers associated with H-type instability in the less diffused vorticity braid. Doubling the jet aspect ratio yields initially thinner shear layers only slightly affected by axisymmetry. The resulting unsteady base flow loses scale selectivity and is prone to a common path of initial transient growth followed by the optimal secondary growth of a wide range of wavenumbers. Increasing both the aspect ratio and the Reynolds number thus yields an even larger secondary growth and a lower wavenumber selectivity. At a lower aspect ratio of $\alpha =5$, the base flow is smooth and a genuine round jet affected by the axisymmetry condition. The axisymmetric modal perturbation of the base flow parallel jet only weakly affects the first common phase of transient growth and the optimal helical perturbation $m=1$ dominates with energy gains considerably larger than those of larger azimuthal wavenumbers whatever the horizon time.

We propose a framework that elucidates the input–output characteristics of flows with complex dynamics arising from nonlinear interactions between different time scales. More specifically, we consider a periodically time-varying base flow, and perform a frequency-domain analysis of periodic perturbations about this base flow. The response of these perturbations is governed by the harmonic resolvent, which is a linear operator similar to the harmonic transfer function introduced by Wereley (1991 Analysis and control of linear periodically time-varying systems, PhD thesis, Massachusetts Institute of Technology). This approach makes it possible to explicitly capture the triadic interactions that are responsible for the energy transfer between different time scales in the flow. For instance, perturbations at frequency $\omega$ are coupled with perturbations at frequency $\alpha$ through the base flow at frequency $\omega -\alpha$. We draw a connection with resolvent analysis, which is a special case of the harmonic resolvent when evaluated about a steady base flow. We show that the left and right singular vectors of the harmonic resolvent are the optimal response and forcing modes, which can be understood as full spatio-temporal signals that reveal space–time amplification characteristics of the flow. Finally, we illustrate the method on examples, including a three-dimensional system of ordinary differential equations and the flow over an airfoil at near-stall angle of attack.

This paper investigates streaks and Görtler vortices in a boundary layer over a flat or concave wall in a contracting or expanding stream, which provides a favourable or adverse pressure gradient, respectively. We consider first the excitation of streaks and Görtler vortices by free stream vortical disturbances (FSVD), and their nonlinear evolution. The focus is on FSVD with sufficiently long wavelength, to which the boundary layer is most receptive. The formulation is directed at the general case where the Görtler number 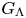$G_{\Lambda }$ (based on the spanwise length scale 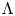$\Lambda$ of FSVD) is of order one, and the FSVD is strong enough that the induced vortices acquire an 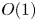$O(1)$ streamwise velocity in the region where the boundary layer thickness becomes comparable with 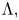$\Lambda,$ and the vortices are governed by the nonlinear boundary region equations (NBRE). An important effect of a pressure gradient is that the oncoming FSVD are distorted by the non-uniform inviscid flow outside the boundary layer through convection and stretching. This process is accounted for by using the rapid distortion theory. The impact of the distorting FSVD is analysed to provide the appropriate initial and boundary conditions, which form, along with the NBRE, the appropriate initial boundary value problem describing the excitation and nonlinear evolution of the vortices. Numerical results show that an adverse/favourable pressure gradient cause the Görtler vortices to saturate earlier/later, but at a lower/higher amplitude than that in the case of zero-pressure-gradient. On the other hand, for the same pressure gradient and at low levels of FSVD, the vortices saturate earlier and at a higher amplitude as 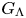$G_{\Lambda }$ increases. Raising FSVD intensity reduces the effects of the pressure gradient and curvature. At a high FSVD level of 14 %, the curvature has no impact on the vortices, while the pressure gradient only influences the saturation intensity. The unsteadiness of FSVD is found to reduce the boundary layer response significantly at FSVD levels, but that effect weakens as the turbulence level increases. A secondary instability analysis of the vortices is performed for moderate adverse and favourable pressure gradients. Three families of unstable modes have been identified, which may become dominant depending on the frequency and streamwise location. In the presence of an adverse pressure gradient, the secondary instability occurs earlier, but the unstable modes appear in a smaller band of frequency, and have smaller growth rates. The opposite is true for a favourable pressure gradient. The present theoretical framework, which accounts for the influence of the curvature, turbulence level and pressure gradient, allows for a detailed and integrated description of the key transition processes, and represents a useful step towards predicting the pretransitional flow and transition itself of the boundary layer over a blade in turbomachinery.

The asymmetries that arise when a mixing layer involves two miscible fluids of differing densities are investigated using incompressible (low-speed) direct numerical simulations. The simulations are performed in the temporal configuration with very large domain sizes, to allow the mixing layers to reach prolonged states of fully turbulent self-similar growth. Imposing a mean density variation breaks the mean symmetry relative to the classical single-fluid temporal mixing layer problem. Unlike prior variable-density mixing layer simulations in which the streams are composed of the same fluids with dissimilar thermodynamic properties, the density variations are presently due to compositional differences between the fluid streams, leading to different mixing dynamics. Variable-density (non-Boussinesq) effects introduce strong asymmetries in the flow statistics that can be explained by the strongest turbulence increasingly migrating to the lighter fluid side as free-stream density difference increases. Interface thickness growth rates also reduce, with some thickness definitions particularly sensitive to the corresponding changes in alignment between density and streamwise velocity profiles. Additional asymmetries in the sense of statistical distributions of densities at a given position within the mixing layer reveal that fine scales of turbulence are preferentially sustained in lighter fluid, which also is where fastest mixing occurs. These effects influence statistics involving density fluctuations, which have important implications for mixing and more complicated phenomena that are sensitive to the mixing dynamics, such as combustion.

Impact of microspheres on liquid surfaces is a universal phenomenon in nature and in industrial processes. However, most relevant studies have mainly focused on the sphere's vertical impact. Herein, we present the first observation on the oblique impact of microspheres on the surface of quiescent liquid using high-speed microphotography. The sphere motion and liquid surface distortion after the oblique impact are basically different from those after a vertical impact. The sphere rotates and its trajectory deviates from the impact direction during the oblique impact process, while the non-axisymmetric liquid surface distortion experiences an evolution from half-cavity to full-cavity patterns. The dependence of motions of the sphere and the three-phase contact line on the impact angle $\alpha$ and Weber number are investigated, and the scaling laws for the sphere's penetration time and penetration depth are given. We provide a phase diagram with respect to the Weber number and impact angle that describes the observed impact modes of submergence and oscillation, which shows that the critical Weber number between two impact modes increases when the impact angle decreases. Additionally, a scaling model is established based on energy balance to distinguish different impact modes. The model indicates that the critical Weber number for the microsphere's oblique impact is equal to $1/{\rm sin}\,\alpha$ times that for vertical impact, agreeing well with the experimental results.

In this research turbulent flow in a ribbed square duct of different blockage ratios ($Br=0.05$, 0.1 and 0.2) at a fixed Reynolds number of $Re_b=5600$ is studied using direct numerical simulation. The results are compared with those of a smooth duct flow. In contrast to the classical two-dimensional rib-roughened boundary-layer flow over a flat plate, the turbulence field is influenced by not only the rib elements but also the four duct sidewalls. The results detail out the three-dimensional effects of the sidewalls and ribs on flow statistics and structures. This study also aims at investigating the effect of blockage ratio on local non-equilibrium of turbulence, large- and small-scale flow anisotropy, and transport of turbulence kinetic energy. It is observed that as the rib height increases, the pressure near the windward face of the rib increases significantly, associated with an accelerated streamwise flow in the duct. Furthermore, an augmentation of the blockage ratio concurrently generates stronger turbulent secondary flow motions, resulting in larger magnitudes of Reynolds stresses near the rib crest. The secondary flow motions drastically alter the turbulent transport processes between the sidewall and duct centre, giving rise to high degrees of non-equilibrium states. The dynamics of coherent structures are studied by examining characteristics of the instantaneous velocity field, swirling strength, temporal auto-correlations, spatial two-point auto-correlations and velocity spectra. The results show that an increase of rib height significantly promotes the ejection and sweep events, which subsequently amplify the strength of vortical motions near the rib crest.

We investigate a mechanism to manipulate wall-bounded flows whereby wave-like undulations of the wall topography drives the creation of bespoke longitudinal vortices. A resonant interaction between the ambient vorticity of the undisturbed shear flow and the undulation of streamlines enforced by the wall topography serves to slightly rotate the spanwise vorticity of the mean flow into the streamwise direction, creating a swirling motion, in the form of regular streamwise rolls. The process is kinematic and essentially identical to the ‘direct drive’ CL1 mechanism for Langmuir circulation (LC) proposed by Craik (J. Fluid Mech., vol. 41, issue 4, 1970, pp. 801–821). Wall shear is modelled by selecting suitable primary flow profiles. A simple, easily integrable expression for the cross-plane streamfunction is found in two asymptotic regimes: the resonant onset of the essentially inviscid instability at early times, and the fully developed steady-state viscous flow. Linear-order solutions for flow over undulating boundaries are obtained, fully analytical in the special case of a power-law profile. These solutions allow us to quickly map out the circulation response to boundary design parameters. The study is supplemented with direct numerical simulations which verify the manifestation of boundary induced Langmuir vortices in laminar flows with no-slip boundaries. Simulations show good qualitative agreement with theory. Quantitatively, the comparisons rest on a displacement length closure parameter adopted in the perturbation theory. While wall-driven LC appear to become unstable in turbulent flows, we propose that the mechanism can promote swirling motion in boundary layers, a flow feature which has been reported to reduce drag in some situations.

A theoretical model based on linear potential flow theory and an eigenfunction matching method is developed to analyse the hydroelastic interaction between water waves and multiple circular floating porous elastic plates. The water domain is divided into the interior and exterior regions, representing the domain beneath each plate and the rest, which extends towards infinity horizontally, respectively. Spatial potentials in these two regions can be expressed as a series expansion of eigenfunctions. Three different types of edge conditions are considered. The unknown coefficients in the potential expressions can be determined by satisfying the continuity conditions for pressure and velocity at the interface of the two regions, together with the requirements for the motion/force at the edge of the plates. Apart from the straightforward method to evaluate the exact power dissipated by the array of porous elastic plates, an indirect method based on Green's theorem is determined. The indirect method expresses the wave-power dissipation in terms of Kochin functions. It is found that wave-power dissipation of an array of circular porous elastic plates can be enhanced by the constructive hydrodynamic interaction between the plates, and there is a profound potential of porous elastic plates for wave-power extraction. The results can be applied to a range of floating structures but have special application in modelling energy loss in flexible ice floes and wave-power extraction by flexible plate wave-energy converters.

We present a novel deterministic model that is capable of predicting particle-to-particle force and torque fluctuations in a fixed bed of randomly distributed monodisperse spheres. First, we generate our dataset by performing particle-resolved direct numerical simulations (PR-DNS) of arrays of stationary spheres in moderately inertial regimes with a Reynolds number range of $2 \leq \textit {Re} \leq 150$ and a solid volume fraction range of $0.1 \leq \phi \leq 0.4$. The key idea exploited by our model is that, while the arrangement of neighbours around each particle is uniform and random, conditioning forces or torques exerted on a reference sphere to specific ranges of values results in the emergence of significantly non-uniform distributions of neighbouring particles. Based on probabilistic arguments, we take advantage of the statistical information extracted from PR-DNS to construct force/torque-conditioned probability distribution maps, which are ultimately used as basis functions for regression. Given the locations of surrounding particles as input to the model, our results demonstrate that the present probability-driven framework is capable of predicting up to 85 % of the actual observed force and torque variation in the best cases. Since the precise location of each particle is known in an Eulerian–Lagrangian (EL) simulation, our model would be able to estimate the unresolved subgrid force and torque fluctuations reasonably well, and thereby considerably enhance the fidelity of EL simulations via improved interphase coupling.

This paper investigates the steady axisymmetric structure of the cold boundary-layer flow surrounding fire whirls developing over localized fuel sources lying on a horizontal surface. The inviscid swirling motion found outside the boundary layer, driven by the entrainment of the buoyant turbulent plume of hot combustion products that develops above the fire, is described by an irrotational solution, obtained by combining Taylor's self-similar solution for the motion in the axial plane with the azimuthal motion induced by a line vortex of circulation $2 {\rm \pi}\Gamma$. The development of the boundary layer from a prescribed radial location is determined by numerical integration for different swirl levels, measured by the value of the radial-to-azimuthal velocity ratio $\sigma$ at the initial radial location. As in the case $\sigma =0$, treated in the seminal boundary-layer analysis of Burggraf et al. (Phys. Fluids, vol. 14, 1971, pp. 1821–1833), the pressure gradient associated with the centripetal acceleration of the inviscid flow is seen to generate a pronounced radial inflow. Specific attention is given to the terminal shape of the boundary-layer velocity near the axis, which displays a three-layered structure that is described by matched asymptotic expansions. The resulting composite expansion, dependent on the level of ambient swirl through the parameter $\sigma$, is employed as boundary condition to describe the deflection of the boundary-layer flow near the axis to form a vertical swirl jet. Numerical solutions of the resulting non-slender collision region for different values of $\sigma$ are presented both for inviscid flow and for viscous flow with moderately large values of the controlling Reynolds number $\Gamma /\nu$. The velocity description provided is useful in mathematical formulations of localized fire-whirl flows, providing consistent boundary conditions accounting for the ambient swirl level.

We use experiments and direct numerical simulations to probe the phase space of low-curvature Taylor–Couette flow in the vicinity of the ultimate regime. The cylinder radius ratio is fixed at $\eta =r_i/r_o=0.91$, where $r_i \, (r_o)$ is the inner (outer) cylinder radius. Non-dimensional shear drivings (Taylor numbers ${\textit {Ta}}$) in the range $10^7\leq {\textit {Ta}}\leq 10^{11}$ are explored for both co- and counter-rotating configurations. In the ${\textit {Ta}}$ range $10^8\leq {\textit {Ta}}\leq 10^{10}$, we observe two local maxima of the angular momentum transport as a function of the cylinder rotation ratio, which can be described as either ‘co-’ or ‘counter-rotating’ due to their location or as ‘broad’ or ‘narrow’ due to their shape. We confirm that the broad peak is accompanied by the strengthening of the large-scale structures, and that the narrow peak appears once the driving (Ta) is strong enough. As first evidenced in numerical simulations by Brauckmann et al. (J. Fluid Mech., vol. 790, 2016, pp. 419–452), the broad peak is produced by centrifugal instabilities and that the narrow peak is a consequence of shear instabilities. We describe how the peaks change with ${\textit {Ta}}$ as the flow becomes more turbulent. Close to the transition to the ultimate regime when the boundary layers (BLs) become turbulent, the usual structure of counter-rotating Taylor vortex pairs breaks down and stable unpaired rolls appear locally. We attribute this state to changes in the underlying roll characteristics during the transition to the ultimate regime. Further changes in the flow structure around ${\textit {Ta}}\approx 10^{10}$ cause the broad peak to disappear completely and the narrow peak to move. This second transition is caused when the regions inside the BLs which are locally smooth regions disappear and the whole boundary layer becomes active.

We present an analytical model of nonlinear evolution of two-dimensional single-mode Rayleigh–Taylor instability (RTI) in cylindrical geometry at arbitrary Atwood number for the first time. Our model covers a full scenario of bubble evolution from the earlier exponential growth to the nonlinear regime with the bubbles growing in time as $\frac {1}{2}a_{b}t^2$ for cylindrical RTI, other than as $V_{b}t$ for planar RTI, where $a_{b}$ and $V_{b}$ are the bubble acceleration and velocity, respectively. It is found that from this model the saturating acceleration $a_{b}$ is formulated as a simplified function of the external acceleration, Atwood number and number of perturbation waves. This model's predictions are in good agreement with data from direct numerical simulations.

The suction force at the leading edge of a round-nosed aerofoil is an important indicator of the state of the flow over the leading edge and, often, the entire aerofoil. The leading-edge suction parameter (LESP) is a non-dimensional version of this force. In recent works, the LESP was calculated with good accuracy for attached flows at low Reynolds numbers (10 000–100 000) from unsteady aerofoil theory. In contrast to this ‘inviscid’ LESP, results from viscous computations and experiments are used here to calculate the ‘viscous’ LESP on aerofoils undergoing pitching motions at low subsonic speeds. The LESP formulation is also updated to account for the net velocity of the aerofoil. Spanning multiple aerofoils, Reynolds numbers and kinematics, the cases include motions in which dynamic stall occurs with or without leading-edge vortex (LEV) formation. Inflections in the surface pressure and skin-friction distributions near the leading edge are shown to be reliable indicators of LEV initiation. Critical LESP, which is the LESP value at LEV initiation, was found to be nearly independent of pivot location, weakly dependent on pitch rate and strongly dependent on Reynolds number. The viscous LESP was seen to drop to near-zero values when the flow is separated at the leading edge, irrespective of LEV formation. This behaviour was shown to correlate well with the loss of streamline curvature at the leading edge due to flow separation. These findings serve to improve our understanding and extend the applicability of the leading-edge suction behaviour gained from earlier works.

This paper considers the diapycnal transport of passive tracers during a Kelvin–Helmholtz mixing event. Numerical simulations of a traditional Kelvin–Helmholtz (KH) configuration of a stratified shear flow are extended to include layers of passive tracer at different locations relative to the shear layer. The evolution of the tracers during the simulation is followed and is analysed using different theoretical approaches. One is to consider the evolution via the distribution in density–tracer space which clearly reveals how the tracers are redistributed across isopycnals by the mixing driven by the growing and saturating KH billow. The shape of the distribution places constraints on the redistribution of the tracer and, for this problem of symmetrically stratified shear, it is shown that the distribution typically tends to a compact form, with significant regions that are nearly linear. The redistribution across isopycnals is also considered via a diffusion equation for the tracer relative to coordinates based on the geometry of density surfaces. The equation is a generalisation of an equation previously derived for transport of density in these coordinates and includes an extra eddy term that arises because there is variation of the tracer along density surfaces. Under certain circumstances and at later stages of the flow, the eddy term can be neglected, and the evolution of the mean tracer profile can be adequately represented using a simple diffusion equation where diffusivity is defined as the effective diffusivity of density, scaled by the molecular diffusion of the tracer.

We develop a stochastic model for Lagrangian velocity as it is observed in experimental and numerical fully developed turbulent flows. We define it as the unique statistically stationary solution of a causal dynamics, given by a stochastic differential equation. In comparison with previously proposed stochastic models, the obtained process is infinitely differentiable at a given finite Reynolds number, and its second-order statistical properties converge to those of an Ornstein–Uhlenbeck process in the infinite Reynolds number limit. In this limit, it exhibits furthermore intermittent scaling properties, as they can be quantified using higher-order statistics. To achieve this, we begin with generalizing the two-layered embedded stochastic process of Sawford (Phys. Fluids A, vol. 3 (6), 1991, pp. 1577–1586) by considering an infinite number of layers. We then study, both theoretically and numerically, the convergence towards a smooth (i.e. infinitely differentiable) Gaussian process. To include intermittent corrections, we follow similar considerations as for the multifractal random walk of Bacry et al. (Phys. Rev. E, vol. 64, 2001, 026103). We derive in an exact manner the statistical properties of this process, and compare them with those estimated from Lagrangian trajectories extracted from numerically simulated turbulent flows. Key predictions of the multifractal formalism regarding the acceleration correlation function and high-order structure functions are also derived. Through these predictions, we understand phenomenologically peculiar behaviours of the fluctuations in the dissipative range, that are not reproduced by our stochastic process. The proposed theoretical method regarding the modelling of infinitely differentiability opens the route to the full stochastic modelling of velocity, including the peculiar action of viscosity on the very fine scales.

Ionization occurs in the upper atmospheres of hot Jupiters and in the interiors of gas giant planets, leading to magnetohydrodynamic (MHD) effects that couple the momentum and the magnetic field, thereby significantly altering the dynamics. In regions of moderate temperatures, the gas is only partially ionized, which also leads to interactions with neutral molecules. To explore the turbulent dynamics of these regions, we utilize partially ionized magnetohydrodynamics (PIMHD), a two-fluid model – one neutral and one ionized – coupled by a collision term proportional to the difference in velocities. Motivated by planetary settings where rotation constrains the large-scale motions to be mostly two-dimensional, we perform a suite of simulations to examine the parameter space of two-dimensional PIMHD turbulence and pay particular attention to collisions and their role in the dynamics, dissipation and energy exchange between the two species. We arrive at, and numerically confirm, an expression for the energy loss due to collisions in both the weakly and strongly collisional limits, and show that, in the latter limit, the neutral fluid couples to the ions and behaves as an MHD fluid. Finally, we discuss some implications of our findings to current understanding of gas giant planet atmospheres.

We study the dynamics of viscous capillary rising in small corners between two curved walls described by a function $y=cx^n$ with $n \ge 1$. Using the Onsager principle, we derive a partial differential equation that describes the time evolution of the meniscus profile. By solving the equation both numerically and analytically, we show that the capillary rising dynamics is quite universal. Our theory explains the surprising finding by Ponomarenko et al. (J. Fluid Mech., vol. 666, 2011, pp. 146–154) that the time dependence of the height not only obeys the universal power-law of $t^{1/3}$, but also that the prefactor is almost independent of $n$.

Pattern-forming instability in various fields is an interesting research topic because of its complex physical nature and numerous applications. In this paper, we experimentally study capillary surface waves and patterns formed on a liquid film, cast on a plane substrate without physical walls, but pinned to the substrate edges, and subjected to multi-axis horizontal (lateral) oscillations (55–333 Hz). The effect of single-axis ultrasonic horizontal vibrations (20–170 kHz) was also investigated. We show that using substrates with different geometrical shapes and various travelling paths created by multi-axis vibrations with a phase angle difference between the axes produce a plethora of standing and travelling wave patterns on the liquid film surface. We report perfect standing square and spiral-like patterns for low-frequency multi-axis horizontal vibrations, which are commonly observed for vertical vibrations, while the mechanisms of momentum transfer to the liquid film from the vibrating substrate are different in vertical and horizontal vibrations. Other patterns forming on the liquid film surface in our experiments include lines/stripes, circles, swirls, pentagons, triangles, etc. It is also reported that low-frequency excitations create harmonic travelling waves and standing patterns, while the frequency of response waves generated by the application of ultrasonic horizontal vibrations is several orders of magnitude less than the excitation frequency. No subharmonic cross-waves are observed in this study, which strengthens the idea that plane substrates (without walls) are a good approximation for the theoretical case of a horizontally vibrated liquid film with infinite lateral length.

Motivated by the results of recent experiments (Kühnen et al., Flow Turbul. Combust., vol. 100, 2018, pp. 919–943), we consider the problem of designing a baffle (an obstacle to the flow) to relaminarise turbulence in pipe flows. Modelling the baffle as a spatial distribution of linear drag ${\boldsymbol {F}}(\boldsymbol {x},t)=-\chi (\boldsymbol {x})\boldsymbol {u}_{tot}(\boldsymbol {x},t)$ within the flow ($\boldsymbol {u}_{tot}$ is the total velocity field and $\chi \ge 0$ a scalar field), two different optimisation problems are considered to design $\chi$ at a Reynolds number $Re=3000$. In the first, the smallest baffle defined in terms of a $L_1$ norm of $\chi$ is sought which minimises the viscous dissipation rate of the flow. In the second, a baffle which minimises the total energy consumption of the flow is treated. Both problems indicate that the baffle should be axisymmetric and radially localised near the pipe wall, but struggle to predict the optimal streamwise extent. A manual search finds an optimal baffle one radius long which is then used to study how the amplitude for relaminarisation varies with $Re$ up to $15\,000$. Large stress reduction is found at the pipe wall, but at the expense of an increased pressure drop across the baffle. Estimates are then made of the break-even point downstream of the baffle where the stress reduction at the wall due to the relaminarised flow compensates for the extra drag produced by the baffle.