doi:10.1017/jfm.2024.1073 Balasubramanian et al. Bursting bubble in an elastoviscoplastic medium
Contents
JFM Papers
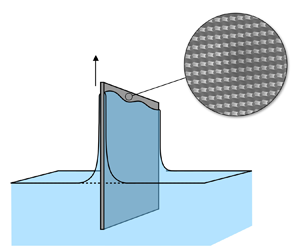
Coating thickness prediction for a viscous film on a rough plate
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2024, A59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
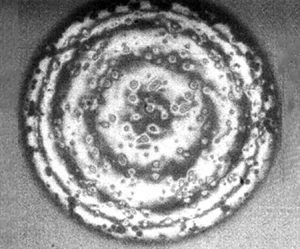
Local spiky contacts during impact of an emulsion drop on a solid surface
-
- Published online by Cambridge University Press:
- 20 December 2024, A60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
Optimisation of the geometry of axisymmetric point-absorber wave energy converters – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 19 December 2024, E1
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 1001 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 January 2025, p. f1
-
- Article
-
- You have access
- Export citation