We derive a mathematical model for steady, unidirectional, thermoelectric magnetohydrodynamic (TEMHD) flow of liquid lithium along a solid metal trench, subject to an imposed heat flux. We use a finite-element method implemented in COMSOL Multiphysics to solve the problem numerically, demonstrating how the fluid velocity, induced magnetic field and temperature change depending on the key physical and geometrical parameters. The observed flow structures are elucidated by using the method of matched asymptotic expansions to obtain approximate solutions in the limit where the Hartmann number is large and the trench walls are thin.

We introduce a new model equation for Stokes gravity waves based on conformal transformations of Euler's equations. The local version of the model equation is relevant for the dynamics of shallow water waves. It allows us to characterize the travelling periodic waves both in the case of smooth and peaked waves and to solve the existence problem exactly, albeit not in elementary functions. Spectral stability of smooth waves with respect to co-periodic perturbations is proven analytically based on the exact count of eigenvalues in a constrained spectral problem.

Despite the extensive research on bubble collapse near rigid walls, the bubble collapse dynamics in the presence of shear flow near a rigid wall is poorly understood. We conduct direct simulations of the Navier–Stokes equations to explore the bubble dynamics and pressures during bubble collapse near a rigid, flat wall under linear shear flow conditions. We examine the dependence of the bubble collapse morphology and wall pressures on the initial bubble location and shear rate. We find that shear distorts the bubble, generating two re-entrant jets – one developing from the side opposite to the mean flow and the other from the far end toward the wall. Upon impact of the jet on the opposite side of the bubble, water-hammer shocks are produced, which propagate outward and interact with the convoluted bubble shape. The shock stretches the bubble towards the wall, resulting in a closer impact location for the jet originating from the far end compared with the case with no shear flow. The water-hammer pressure location can be approximated as the theoretical distance travelled by a particle initialised at the bubble centre with the corresponding constant shear flow velocity. The maximum wall pressures can thus be predicted by considering the distance between the far jet impingement location and the wall along the wall-normal direction. As the shear rate is increased, the maximum wall pressure increases, although only marginally. We determine the critical initial stand-off distance from the wall at which the bubble morphology is shear dominated, i.e. characterised by converging re-entrant jets.

The controllability of passive microparticles that are advected with the fluid flow generated by an actively controlled one is studied. The particles are assumed to be suspended in a viscous fluid and well separated so that the far-field Stokes flow solutions may be used to describe their interactions. Explicit elementary moves parametrized by an amplitude $\varepsilon >0$ are devised for the active particle. Applying concepts from geometric control theory, the leading-order resulting displacements of the passive particles in the limit $\varepsilon \to 0$ are used to propose strategies for moving one active particle and one or two passive particles, proving controllability in such systems. The leading-order (in $\varepsilon$) theoretical predictions of the particle displacements are compared with those obtained numerically and it is found that the discrepancy is small even when $\varepsilon \approx 1$. These results demonstrate the potential for a single actuated particle to perform complex micromanipulations of passive particles in a suspension.

Particle-laden flow through conduits is ubiquitous in both natural and industrial systems. In such flows, particles often migrate across the main fluid stream, resulting in non-uniform spatial distribution owing to particle–fluid and particle–particle interactions. The most relevant lateral particle migration mechanism by particle–fluid interaction is the Segré–Silberberg effect, which is induced by the inertial forces exerted on a particle, as the flow rate increases. However, methods to suppress it have not been suggested yet. Here, we demonstrate that adding a small amount of polymer to the particle-suspending solvent effectively suppresses the Segré–Silberberg effect in a square channel. To accurately determine the position of the particles within the channel cross-sections, we devised a dual-view imaging system applicable to microfluidic systems. Our analyses show that the Segré–Silberberg effect is effectively suppressed in a square microchannel due to the balance between the inertial and elastic forces at an optimal polymer concentration while maintaining nearly constant shear viscosity.

This study identifies two previously unrecognised screech modes in non-axisymmetric jets. Spectral proper orthogonal decomposition (SPOD) of ultra-high-speed schlieren images reveals a bi-axial flapping mode in a rectangular jet and a quasi-helical mode in an elliptical jet. To educe the complex three-dimensional structure of these new modes, SPOD is performed on datasets from different viewing perspectives, produced by rotating the nozzle with respect to the schlieren path to an azimuthal angle $\theta$. The bi-axial flapping mode is strongly antisymmetric from any perspective. However, the SPOD eigenvalue at the screech frequency ($\lambda _s$) varies with $\theta$ and the axial distance of the SPOD domain from the nozzle lip. This mode most closely resembles a flapping mode in the minor-axis plane close to the nozzle lip and a wagging mode in the major-axis plane further downstream. This transition from flapping to wagging at the same frequency correlates with the axis switching defined by the shock-cell structure in the mean flow. The quasi-helical mode in the elliptical jet is characterised by an antisymmetric structure present in the SPOD spatial modes whose eigenvalue $\lambda _s$ is insensitive to both $\theta$ and the axial domain. These findings indicate that the spatial evolution of the mean flow in non-axisymmetric jets may allow them to support a range of additional screech modes that differ significantly from those supported by the original three-dimensional shape of the jet.

The three-dimensional flow field past an I-shaped dual-step cylinder has been obtained by numerical integration of the Navier–Stokes equations at Reynolds number ($Re_D$) 150. The I-shaped cylinder consisted of two large-diameter (D) cylinders with a small-diameter (d) cylinder in between. With a view to exploring the vortex dynamics and structural loads, simulations were performed for eight different lengths $l$ of the small cylinder, varied from $l/D=10$ to 0.2 for a fixed diameter ratio $D/d=2$. When the length of the small cylinder is sufficiently large, the wake behind the I-shaped cylinder is similar to the wake behind the single-step cylinder (Tian et al., J. Fluid Mech., vol. 891, 2020, A24). As the small cylinder length decreases, the enhanced interactions between the two steps make the present wake deviate from the wake of the single-step cylinder, leading to four different wake modes distinguished by different combinations of vortex cells. The physical formation mechanisms were analysed in terms of the vortex dynamics. Besides the wake flow, the streamwise vortices around the I-shaped step cylinder were also investigated. A pair of edge vortices and a junction vortex were identified for $l/D \geq ~1$. When the gap between the two steps becomes too small, $l/D \leq ~0.2$, the junction vortex disappears, and only a pair of edge vortices exists. Varying the distance between the two steps strongly affects the structural loads (drag and lift) along the I-shaped cylinder. The dependence of the loads on $l/D$ was readily explained by the different wake modes.

Understanding the mechanisms behind the remote triggering of landslides by seismic waves at micro-strain amplitude is essential for quantifying seismic hazards. Granular materials provide a relevant model system to investigate landslides within the unjamming transition framework, from solid to liquid states. Furthermore, recent laboratory experiments have revealed that ultrasound-induced granular avalanches can be related to a reduction in the interparticle friction through shear acoustic lubrication of the contacts. However, investigating slip at the scale of grain contacts within an optically opaque granular medium remains a challenging issue. Here, we propose an original coupling model and numerically investigate two-dimensional dense granular flows triggered by basal acoustic waves. We model the triggering dynamics at two separated time scales – one for grain motion (milliseconds) and the other for ultrasound (10 ${\rm \mu} {\rm s}$) – relying on the computation of vibrational modes with a discrete element method through the reduction of the local friction. We show that ultrasound predominantly propagates through the strong-force chains, while the ultrasound-induced decrease of interparticle friction occurs in the weak contact forces perpendicular to the strong-force chains. This interparticle friction reduction initiates local rearrangements at the grain scale that eventually lead to a continuous flow through a percolation process at the macroscopic scale – with a delay depending on the proximity to the failure. Consistent with experiments, we show that ultrasound-induced flow appears more uniform in space than pure gravity-driven flow, indicating the role of an effective temperature by ultrasonic vibration.

A liquid drop impacting a rigid substrate undergoes deformation and spreading due to normal reaction forces, which are counteracted by surface tension. On a non-wetting substrate, the drop subsequently retracts and takes off. Our recent work (Zhang et al., Phys. Rev. Lett., vol. 129, 2022, 104501) revealed two peaks in the temporal evolution of the normal force 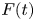$F(t)$ – one at impact and another at jump-off. The second peak coincides with a Worthington jet formation, which vanishes at high viscosities due to increased viscous dissipation affecting flow focusing. In this article, using experiments, direct numerical simulations and scaling arguments, we characterize both the peak amplitude 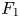$F_1$ at impact and the one at takeoff (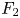$F_2$) and elucidate their dependency on the control parameters: the Weber number 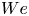$We$ (dimensionless impact kinetic energy) and the Ohnesorge number 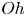$Oh$ (dimensionless viscosity). The first peak amplitude 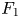$F_1$ and the time 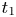$t_1$ to reach it depend on inertial time scales for low viscosity liquids, remaining nearly constant for viscosities up to 100 times that of water. For high viscosity liquids, we balance the rate of change in kinetic energy with viscous dissipation to obtain new scaling laws: 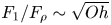$F_1/F_\rho \sim \sqrt {Oh}$ and 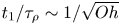$t_1/\tau _\rho \sim 1/\sqrt {Oh}$, where 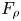$F_\rho$ and 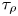$\tau _\rho$ are the inertial force and time scales, respectively, which are consistent with our data. The time 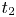$t_2$ at which the amplitude 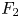$F_2$ appears is set by the inertiocapillary time scale 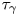$\tau _\gamma$, independent of both the viscosity and the impact velocity of the drop. However, these properties dictate the magnitude of this amplitude.

Hydrodynamic consequences of using simpler geometric shapes to represent coral canopies are examined through a laboratory study. A canopy composed of cylinders is compared with a canopy composed of 3-D-printed, scaled down coral heads in a recirculating flume. Vertical velocity profiles are measured at four horizontal locations for each canopy type, and mean velocity and turbulence statistics are compared both within and above the canopy. A narrow, defined wake on the scale of the canopy element is present behind the cylinder canopy elements that is absent in the coral canopy. There is also a peak in shear stress at the top of the cylinder canopy, likely due to the sharp edge at the top of the cylinder. Above the canopy, however, turbulence statistics and friction velocities behave similarly for both canopy types. Therefore, the results indicate we may reasonably get coral reef drag estimates from canopies with simpler geometric surrogates, especially when the mean free-stream and within-canopy flow speeds are matched to environmental conditions.