We investigate numerically the transitions and oscillatory regimes in two-layer quasigeostrophic hetons and tripoles composed of patches of uniform potential vorticity (PV). The contour-surgery algorithms are employed, in which either some symmetries are preserved, or asymmetric evolution of the vortex structures is allowed, induced by generally asymmetric numerical noise. The fluid layers are assumed equally thick. First, the evolution of hetons is considered. A heton, a steadily translating pair of vortices residing in different layers, is antisymmetric in the sense that the two PV patches are opposite in sign and symmetric in shape about the axis of translation. A feebly stable heton, when exposed to weak antisymmetric perturbations, responds by developing an oscillation, which culminates in a transition to a new, substantially robust oscillating heton. The results obtained reinforce our earlier findings regarding the modon-to-modon transition (Kizner et al., J. Fluid Mech., vol. 468, 2002, pp. 239–270; Kizner, Phys. Fluids, vol. 18 (5), 2006, 056601; Kizner, UTAM Symposium on Hamiltonian Dynamics, Vortex Structures, Turbulence (ed. Borisov et al.), IUTAM Bookseries, vol. 6, 2008, pp. 125–133. Springer) and clarify the transition mechanism. Asymmetric perturbations might cause a heton-to-tripole transition. Next we consider the transitions and oscillations in carousel tripoles exposed to weak, generally asymmetric perturbations. A carousel tripole is a steadily rotating centrally symmetric ensemble of three PV patches, with the central vortex being located in one layer and the two remaining, satellite vortices in the other layer. Depending on the tripoles’ size, hence also on the shape of the satellite vortices, three different types of transition are revealed, the transition to a ringed (shielded) monopole being one of them. Whereas the transition of a ringed monopole into a tripole is a known phenomenon, the reverse transition in baroclinic flows is detected for the first time.
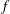 $f$-plane approximation: singularity in the large-scale limit
$f$-plane approximation: singularity in the large-scale limit