The theory of magnetohydrodynamic (MHD) turbulence predicts that Alfvénic and slow-mode-like compressive fluctuations are energetically decoupled at small scales in the inertial range. The partition of energy between these fluctuations determines the nature of dissipation, which, in many astrophysical systems, happens on scales where plasma is collisionless. However, when the magnetorotational instability (MRI) drives the turbulence, it is difficult to resolve numerically the scale at which both types of fluctuations start to be decoupled because the MRI energy injection occurs in a broad range of wavenumbers, and both types of fluctuations are usually expected to be coupled even at relatively small scales. In this study, we focus on collisional MRI turbulence threaded by a near-azimuthal mean magnetic field, which is naturally produced by the differential rotation of a disc. We show that, in such a case, the decoupling scales are reachable using a reduced MHD model that includes differential-rotation effects. In our reduced MHD model, the Alfvénic and compressive fluctuations are coupled only through the linear terms that are proportional to the angular velocity of the accretion disc. We numerically solve for the turbulence in this model and show that the Alfvénic and compressive fluctuations are decoupled at the small scales of our simulations as the nonlinear energy transfer dominates the linear coupling below the MRI-injection scale. In the decoupling scales, the energy flux of compressive fluctuations contained in the small scales is almost double that of Alfvénic fluctuations. Finally, we discuss the application of this result to prescriptions of ion-to-electron heating ratio in hot accretion flows.

Extreme-ultraviolet pulses can propagate through ionised solid-density targets, unlike optical pulses and, thus, have the potential to probe the interior of such plasmas on sub-femtosecond timescales. We present a synthetic diagnostic method for solid-density laser-generated plasmas based on the dispersion of an extreme-ultraviolet attosecond probe pulse, in a pump–probe scheme. We demonstrate the theoretical feasibility of this approach through calculating the dispersion of an extreme-ultraviolet probe pulse propagating through a laser-generated plasma. The plasma dynamics is calculated using a particle-in-cell simulation, whereas the dispersion of the probe is calculated with an external pseudo-spectral wave solver, allowing for high accuracy when calculating the dispersion. The application of this method is illustrated on thin-film plastic and aluminium targets irradiated by a high-intensity pump pulse. By comparing the dispersion of the probe pulse at different delays relative to the pump pulse, it is possible to follow the evolution of the plasma as it disintegrates. The high-frequency end of the dispersion provides information on the line-integrated electron density, whereas lower frequencies are more affected by the highest density encountered along the path of the probe. In addition, the presence of thin-film interference could be used to study the evolution of the plasma surface.

Recently, the collisionless pitch-angle scattering for relativistic runaway electrons (REs) in toroidal geometries such as tokamaks was discovered through a full orbit simulation approach (Liu et al., Nucl. Fusion, vol. 56, 2016, p. 064002), and it was then theoretically investigated that a new expression for the magnetic moment, including the second-order corrections, could essentially reproduce the so-called collisionless pitch-angle scattering process (Liu et al., Nucl. Fusion, vol. 58, 2018, p. 106018). In this paper, with synchrotron radiation, extensive numerical verification of the validity of the high-order guiding-centre theory is given for simulations involving REs by incorporating such an expression for the magnetic moment into our particle tracing code. A high-order guiding-centre simulation approach with synchrotron radiation (HGSA) is applied. Synchrotron radiation plays an essential role in the life cycle of REs. The energy of REs first increases and then becomes saturated until the electric field acceleration is balanced by the radiation dissipation. Unfortunately, the process cannot be simulated accurately with the standard guiding-centre model, i.e. the first-order guiding-centre model. Remarkably, it is found that the HGSA can effectively produce the fundamental process of REs. Since the time scale of the energy saturation of REs is close to seconds, the computational cost becomes significant. In order to save costs, it is necessary to estimate the time of energy saturation. An analytical estimate is derived for the time it takes for synchrotron drag to balance an accelerating electric field and the provided formula has been numerically verified. Test calculations reveal that HGSA is favourable for exploiting the dynamics of REs in tokamak plasmas.

The kinetic–magnetohydrodynamic (MHD) hybrid simulation approach for macroscopic instabilities in plasmas can be extended to include the kinetic effects of both thermal ions and energetic ions. The new coupling scheme includes synchronization of the density and parallel velocity between thermal ions and MHD, in addition to pressure coupling, to ensure the quasineutrality condition and avoid numerical errors. The new approach has been implemented in the kinetic-MHD code M3D-C1-K, and was used to study the thermal ion kinetic effects and Landau damping in fishbone modes in both DIII-D and NSTX. It is found that the thermal ion kinetic effects can cause an increase of the frequencies of the non-resonant $n=1$ fishbone modes driven by energetic particles for $q_\mathrm {min}>1$, and Landau damping can provide additional stabilization effects. A nonlinear simulation for $n=1$ fishbone mode in NSTX is also performed, and the perturbation on magnetic flux surfaces and the transport of energetic particles are calculated.

Electromagnetic (EM) instabilities and turbulence driven by the electron-temperature gradient (ETG) are considered in a local slab model of a tokamak-like plasma. Derived in a low-beta asymptotic limit of gyrokinetics, the model describes perturbations at scales both larger and smaller than the electron inertial length $d_e$, but below the ion Larmor scale $\rho _i$, capturing both electrostatic and EM regimes of turbulence. The well-known electrostatic instabilities – slab and curvature-mediated ETG – are recovered, and a new instability is found in the EM regime, called the thermo-Alfvénic instability (TAI). It exists in both a slab version (sTAI, destabilising kinetic Alfvén waves) and a curvature-mediated version (cTAI), which is a cousin of the (electron-scale) kinetic ballooning mode. The cTAI turns out to be dominant at the largest scales covered by the model (greater than $d_e$ but smaller than $\rho _i$), its physical mechanism hinging on the fast equalisation of the total temperature along perturbed magnetic field lines (in contrast to kinetic ballooning mode, which is pressure balanced). A turbulent cascade theory is then constructed, with two energy-injection scales: $d_e$, where the drivers are slab ETG and sTAI, and a larger (parallel system size dependent) scale, where the driver is cTAI. The latter dominates the turbulent transport if the temperature gradient is greater than a certain critical value, which scales inversely with the electron beta. The resulting heat flux scales more steeply with the temperature gradient than that due to electrostatic ETG turbulence, giving rise to stiffer transport. This can be viewed as a physical argument in favour of near-marginal steady-state in electron-transport-controlled plasmas (e.g. the pedestal). While the model is simplistic, the new physics that is revealed by it should be of interest to those attempting to model the effect of EM turbulence in tokamak-relevant configurations with high beta and large ETGs.

We extend our previous work on the two-dimensional (2-D) Dimits transition in ion-scale turbulence (Ivanov et al., J. Plasma Phys., vol. 86, 2020, 855860502) to include variations along the magnetic field. We consider a three-field fluid model for the perturbations of electrostatic potential, ion temperature, and ion parallel flow in a constant-magnetic-curvature geometry without magnetic shear. It is derived in the cold-ion, long-wavelength asymptotic limit of the gyrokinetic theory. Just as in the 2-D model, a low-transport (Dimits) regime exists and is found to be dominated by a quasistatic staircase-like arrangement of strong zonal flows and zonal temperature. This zonal staircase is formed and maintained by a negative turbulent viscosity for the zonal flows. Unlike the 2-D model, the three-dimensional (3-D) one does not suffer from an unphysical blow up beyond the Dimits threshold where the staircase becomes nonlinearly unstable. Instead, a well-defined finite-amplitude saturated state is established. This qualitative difference between the 2-D and 3-D models is due to the appearance of small-scale ‘parasitic’ modes that exist only if we allow perturbations to vary along the magnetic field lines. These modes extract energy from the large-scale perturbations and provide an effective enhancement of large-scale thermal diffusion, thus aiding the energy transfer from large injection scales to small dissipative ones. We show that in our model, the parasitic modes always favour a zonal-flow-dominated state. In fact, a Dimits state with a zonal staircase is achieved regardless of the strength of the linear drive, provided the system is sufficiently extended along the magnetic field and sufficient parallel resolution is provided.

The stability properties of kinetic ballooning modes are investigated for a number of magnetic configurations of the stellarator Wendelstein 7-X. In particular, we consider the effects of the vacuum rotational transform, ${\raise.1pt-\kern-6pt\iota}$, and the mirror ratio. The analysis sheds light on the interplay between global magnetohydrodynamic configuration properties and local gyrokinetic stability, and is instrumental in the design of high-$\beta$ (the ratio of kinetic to magnetic pressure) operation scenarios. In particular, it is demonstrated that some Wendelstein 7-X magnetic configurations have a relatively low kinetic ballooning mode threshold.

Understanding generation and mitigation of runaway electrons in disruptions is important for the safe operation of future tokamaks. In this paper we investigate the runaway dynamics in reactor-scale spherical tokamaks, focusing on a compact nominal design with a plasma current of 21 megaamperes (MA), 1.8 T magnetic field on axis and major radius of approximately 3 m. We study both the severity of runaway generation during unmitigated disruptions, and the effect that typical mitigation schemes based on massive material injection have on runaway production. The study is conducted using the numerical framework dream (Disruption Runaway Electron Analysis Model). We find that, in many cases, mitigation strategies are necessary to prevent the runaway current from reaching multi-MA levels. Our results indicate that, with a suitably chosen deuterium–neon mixture for mitigation, it is possible to achieve a tolerable runaway current and ohmic current evolution. However, this does not account for the runaway source due to wall activation, which has been found to severely limit successful mitigation at conventional aspect ratios, but whose definition requires a more complete wall specification. Furthermore, the majority of the thermal energy loss is found to happen through radial transport rather than radiation, which poses a risk of unacceptable localised heat loads.

In fusion devices, the geometry of the confining magnetic field has a significant impact on the instabilities that drive turbulent heat loss. This is especially true of stellarators, where the density-gradient-driven branch of the ‘trapped electron mode’ (TEM) is predicted to be linearly stable if the magnetic field has the maximum-J property, as is very approximately the case in certain magnetic configurations of the Wendelstein 7-X experiment (W7-X). Here we show, using both analytical theory and simulations, that the benefits of the optimisation of W7-X also serve to mitigate ion-temperature-gradient (ITG) modes as long as an electron density gradient is present. We find that the effect indeed carries over to nonlinear numerical simulations, where W7-X has low TEM-driven transport, and reduced ITG turbulence in the presence of a density gradient, giving theoretical support for the existence of enhanced confinement regimes, in the presence of strong density gradients (e.g. hydrogen pellet or neutral beam injection).

We introduce modes of instantaneous optimal growth of free energy for the fully electromagnetic gyrokinetic equations. We demonstrate how these ‘optimal modes’ arise naturally from the free energy balance equation, allowing its convenient decomposition, and yielding a simple picture of energy flows. Optimal modes have a number of other favourable features, such as their low dimensionality, efficiency of computation and the fact that their growth rates provide a rigorous and ‘tight’ upper bound on both the nonlinear growth rate of energy, and the linear growth rate of traditional gyrokinetic (normal mode) instabilities. We provide simple closed-form solutions for the optimal growth rates in a number of asymptotic limits, and compare these with our previous bounds.

Using two-dimensional particle-in-cell simulations of collsionless plasmoid instability, the spatial and temporal variations of electric field components are investigated. The initial magnetic field is a Harris sheet which is added by a non-uniform perpendicular magnetic field (guide field). The effects of weak and medium guide field on the evolution of plasmoid instability and associated electric field are discussed with the input parameters of the solar corona with the condition $\omega _{{\rm pe}}/\omega _{{\rm ce}}>1$. As the current sheet elongates, magnetic reconnection in an X-point transits into the plasmoid instability, in which secondary X-points are formed and the consequent magnetic islands coalesce and form larger islands. During the instability, electric field components show two types of disturbances. (1) Transient waves, being excited very early, propagate mainly perpendicular to the current sheet and become damped as the instability proceeds to the nonlinear stage. Fourier analysis reveals that electromagnetic right- and left-hand polarized modes parallel to the initial magnetic field and also the extraordinary mode perpendicular to the current sheet are excited. Additionally, electron Langmuir and slow magnetosonic waves are observed in both directions. (2) Inside the current sheet, an electric field is generated by the plasmoid-dominated reconnection and grows in amplitude as the plasmoid instability proceeds. Moreover, in our study, the effects of amplitude-varying guide field on the spatial structure of electric field components outside and inside the current sheet are discussed. This study is valuable because understanding the spatial and temporal variation of the electric field is an essential prerequisite for the issue of particle acceleration in plasmoid-dominated magnetic reconnection.

Plasma-terminating disruptions in future fusion reactors may result in conversion of the initial current to a relativistic runaway electron beam. Validated predictive tools are required to optimise the scenarios and mitigation actuators to avoid the excessive damage that can be caused by such events. Many of the simulation tools applied in fusion energy research require the user to specify input parameters that are not constrained by the available experimental information. The conventional approach, where an expert modeller calibrates these input parameters based on domain knowledge, is prone to lead to an intractable validation challenge without systematic uncertainty quantification. Bayesian inference algorithms offer a promising alternative approach that naturally includes uncertainty quantification and is less subject to user bias in choosing the input parameters. The main challenge in using these methods is the computational cost of simulating enough samples to construct the posterior distributions for the uncertain input parameters. This challenge can be overcome by combining probabilistic surrogate modelling, such as Gaussian process regression, with Bayesian optimisation, which can reduce the number of required simulations by several orders of magnitude. Here, we implement this type of Bayesian optimisation framework for a model for analysis of disruption runaway electrons, and explore for simulations of current quench in a JET plasma discharge with an argon induced disruption. We use this proof-of-principle framework to explore the optimum input parameters with uncertainties in optimisation tasks ranging from one to seven dimensions. The relevant Python codes that are used in the analysis are available via https://github.com/aejarvin/BO_FOR_RE_SIMULATIONS/.

New orbit-averaged equations for low collisionality neoclassical fluxes in large aspect ratio stellarators with mirror ratios close to unity are derived. The equations retain finite orbit width effects by employing the second adiabatic invariant $J$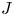 as a velocity-space coordinate and they have been implemented in the orbit-averaged neoclassical code KNOSOS (Velasco et al., J. Comput. Phys., vol. 418, 2020, 109512; Velasco et al., Nucl. Fusion, vol. 61, 2021, 116013). The equations are used to study the $1/\nu$ 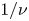regime and the lower collisionality regimes. For generic large aspect ratio stellarators with mirror ratios close to unity, as the collision frequency decreases, the $1/\nu$ 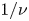regime transitions directly into the $\nu$ 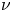regime, without passing through a $\sqrt {\nu }$ 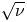regime. An explicit formula for the neoclassical fluxes in the $\nu$ 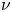regime is obtained. The formula includes the effect of particles that transition between different types of wells. While these transitions produce stochastic scattering independent of the value of the collision frequency in velocity space, the diffusion in real space remains proportional to the collision frequency. The $\sqrt {\nu }$ 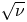regime is only recovered in large aspect ratio stellarators close to omnigeneity: large aspect ratio stellarators with large mirror ratios and optimized large aspect ratio stellarators with mirror ratios close to unity. Neoclassical transport in large aspect ratio stellarators with large mirror ratios can be calculated with the orbit-averaged equations derived by Calvo et al. (Plasma Phys. Control. Fusion, vol. 59, 2017, 055014). In these stellarators, the $\sqrt {\nu }$ 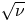regime exists in the collisionality interval $(a/R) \ln (R/a) \ll \nu _{ii} R a/\rho _i v_{ti} \ll R/a$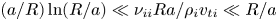. In optimized large aspect ratio stellarators with mirror ratios close to unity, the $\sqrt {\nu }$ 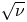regime occurs in an interval of collisionality that depends on the deviation from omnigeneity $\delta$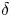: $\delta ^{2} |\ln \delta | \ll \nu _{ii} R a/\rho _i v_{ti} \ll 1$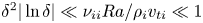. Here, $\nu _{ii}$ 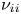is the ion–ion collision frequency, $\rho _i$ 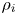and $v_{ti}$ 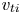are the ion gyroradius and thermal speed, and $a$ 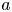and $R$ 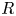are the minor and major radii.

Following indirect-drive experiments which demonstrated promising performance for low convergence ratios (below 17), previous direct-drive simulations identified a fusion-relevant regime which is expected to be robust to hydrodynamic instability growth. This paper expands these results with simulated implosions at lower energies of 100 and 270 kJ, and ‘hydrodynamic equivalent’ capsules which demonstrate comparable convergence ratio, implosion velocity and in-flight aspect ratio without the need for cryogenic cooling, which would allow the assumptions of one-dimensional-like performance to be tested on current facilities. A range of techniques to improve performance within this regime are then investigated, including the use of two-colour and deep ultraviolet laser pulses. Finally, further simulations demonstrate that the deposition of electron energy into the hotspot of a low convergence ratio implosion through auxiliary heating also leads to significant increases in yield. Results include break even for 1.1 MJ of total energy input (including an estimated 370 kJ of short-pulse laser energy to produce electron beams for the auxiliary heating), but are found to be highly dependent upon the efficiency with which electron beams can be created and transported to the hotspot to drive the heating mechanism.

Magnetic reconnection, especially in the relativistic regime, provides an efficient mechanism for accelerating relativistic particles and thus offers an attractive physical explanation for non-thermal high-energy emission from various astrophysical sources. I present a simple analytical model that elucidates key physical processes responsible for reconnection-driven relativistic non-thermal particle acceleration in the large-system, plasmoid-dominated regime in two dimensions. The model aims to explain the numerically observed dependencies of the power-law index $p$ and high-energy cutoff $\gamma _c$ of the resulting non-thermal particle energy spectrum $f(\gamma )$ on the ambient plasma magnetization $\sigma$, and (for $\gamma _c$) on the system size $L$. In this self-similar model, energetic particles are continuously accelerated by the out-of-plane reconnection electric field $E_{\rm rec}$ until they become magnetized by the reconnected magnetic field and eventually trapped in plasmoids large enough to confine them. The model also includes diffusive Fermi acceleration by particle bouncing off rapidly moving plasmoids. I argue that the balance between electric acceleration and magnetization controls the power-law index, while trapping in plasmoids governs the cutoff, thus tying the particle energy spectrum to the plasmoid distribution.

A spontaneous heating process is found to arise in a system where a magnetic island is present due to a linearly unstable tearing mode. The parity, the relative phases and the structure of the fields determined linearly by the tearing mode cause the compression of the plasma in the direction parallel to the magnetic field to heat the plasma in the vicinity of the separatrix in the nonlinear phase. Using a six-field electromagnetic fluid model, the process is found to be present in both two-dimensional single-helicity and three-dimensional multi-helicity simulations with both symmetric and asymmetric magnetic equilibrium profiles. A noteworthy feature of the model is that the higher-order compression terms responsible for the heating process are retained in the equations. The process is believed to be linked to experimental observations of localized hot-spots on externally induced magnetic islands.

Small-amplitude, symmetry-breaking magnetic field perturbations, including resonant magnetic perturbations (RMPs) and error fields, can profoundly impact plasma properties in both tokamaks and stellarators. In this work, we perform the first comparison between the Stepped Pressure Equilibrium Code (SPEC) (a comparatively fast and efficient equilibrium code based on energy-minimisation principles) and M3D-C$^{1}$ (a high-fidelity albeit computationally expensive initial-value extended-magnetohydro- dynamic (MHD) code) to assess the conditions under which SPEC can be used to model the nonlinear, non-ideal plasma response to an externally applied $(m=2,n=1)$ RMP field in an experimentally relevant geometry. We find that SPEC is able to capture the plasma response in the weakly nonlinear regime – meaning perturbation amplitudes below the threshold for break up of the separatrix and onset of secondary magnetic island formation – when around half of the total toroidal flux is enclosed in the volume containing the $q=2$ resonant surface. The observed dependence of SPEC solutions on input parameters, including toroidal flux and the number of volumes into which the plasma is partitioned, indicates that additional exploration of the underlying Multi-Region Relaxed MHD physics model is needed to constrain the choice of parameters. Nonetheless, this work suggests promising applications of SPEC to optimisation and fusion plasma design.