A drift-kinetic calculation in an axisymmetric tokamak, with super-diamagnetic flows, is presented to elucidate the relation between the radial electric field, 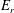 $E_{r}$, zonal flows and the rapid precession of the trapped particle (TP) population. It has been shown earlier (Rosenbluth & Hinton, Phys. Rev. Lett., vol. 80(4), 1998, p. 724, hereafter RH) that an initial radial electric field results in geodesic acoustic mode oscillations which subsequently Landau damp, resulting in a much smaller final residual electric field, and accompanying parallel zonal flows. We observe an apparent paradox: the final angular momentum in the RH parallel zonal flow is much smaller than the angular momentum expected from the well-known rapid precession of the trapped particle population in the RH residual electric field. We reconcile this paradox by illuminating the presence of a population of reverse circulating particle flows that, dominantly, are equal and opposite to the rapid TP precession. Mathematically, the calculation is facilitated by transforming to an energy coordinate shifted from conventional by an amount proportional to
$E_{r}$, zonal flows and the rapid precession of the trapped particle (TP) population. It has been shown earlier (Rosenbluth & Hinton, Phys. Rev. Lett., vol. 80(4), 1998, p. 724, hereafter RH) that an initial radial electric field results in geodesic acoustic mode oscillations which subsequently Landau damp, resulting in a much smaller final residual electric field, and accompanying parallel zonal flows. We observe an apparent paradox: the final angular momentum in the RH parallel zonal flow is much smaller than the angular momentum expected from the well-known rapid precession of the trapped particle population in the RH residual electric field. We reconcile this paradox by illuminating the presence of a population of reverse circulating particle flows that, dominantly, are equal and opposite to the rapid TP precession. Mathematically, the calculation is facilitated by transforming to an energy coordinate shifted from conventional by an amount proportional to 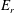 $E_{r}$. We also discuss the well-known RH coefficient in the context of effective mass and show how the TP precession and the opposite circulating flows contribute to this mass. Finally, we show that in the long wavelength limit, the RH flows and RH coefficient arise as a natural consequence of conservation of toroidal angular momentum and the second adiabatic invariant.
$E_{r}$. We also discuss the well-known RH coefficient in the context of effective mass and show how the TP precession and the opposite circulating flows contribute to this mass. Finally, we show that in the long wavelength limit, the RH flows and RH coefficient arise as a natural consequence of conservation of toroidal angular momentum and the second adiabatic invariant.
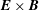 $\boldsymbol{E}\times \boldsymbol{B}$ weak turbulence transport
$\boldsymbol{E}\times \boldsymbol{B}$ weak turbulence transport