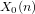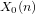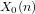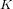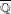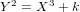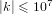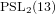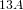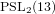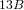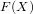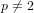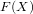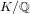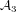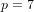Contents
Research Article
Computing functions on Jacobians and their quotients
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 555-577
-
- Article
-
- You have access
- Export citation
Hyperelliptic modular curves
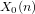 $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
$X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 578-602
-
- Article
-
- You have access
- Export citation
A quasi-linear time algorithm for computing modular polynomials in dimension 2
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2015, pp. 603-632
-
- Article
-
- You have access
- Export citation
Mordell’s equation: a classical approach
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
A software package for Mori dream spaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 November 2015, pp. 647-659
-
- Article
-
- You have access
- Export citation
Withdrawn
Oscillation of differential equations with non-monotone retarded arguments
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 660-666
-
- Article
-
- You have access
- Export citation
Research Article
Every
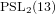 $\text{PSL}_{2}(13)$ in the Monster contains
$\text{PSL}_{2}(13)$ in the Monster contains 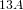 $13A$ -elements
$13A$ -elements
- Part of:
-
- Published online by Cambridge University Press:
- 01 November 2015, pp. 667-674
-
- Article
-
- You have access
- Export citation
Two compact incremental prime sieves
- Part of:
-
- Published online by Cambridge University Press:
- 01 November 2015, pp. 675-683
-
- Article
-
- You have access
- Export citation
On
 ${\it\lambda}$ -invariants attached to cyclic cubic number fields
${\it\lambda}$ -invariants attached to cyclic cubic number fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 684-698
-
- Article
-
- You have access
- Export citation
Good families of Drinfeld modular curves
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
A parallel root-finding algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 713-729
-
- Article
-
- You have access
- Export citation
A computational iterative method for solving nonlinear ordinary differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 730-753
-
- Article
-
- You have access
- Export citation
CoxIter – Computing invariants of hyperbolic Coxeter groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 754-773
-
- Article
-
- You have access
- Export citation