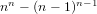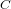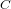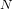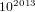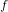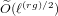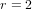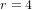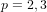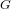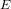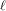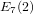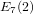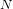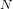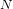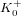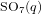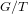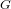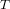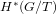Contents
Research Article
Finite basis problem for semigroups of order six
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2015, pp. 1-129
-
- Article
-
- You have access
- Export citation
McCammond’s normal forms for free aperiodic semigroups revisited
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2015, pp. 130-147
-
- Article
-
- You have access
- Export citation
Squarefree values of trinomial discriminants
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2015, pp. 148-169
-
- Article
-
- You have access
- Export citation
Genus-2 curves and Jacobians with a given number of points
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2015, pp. 170-197
-
- Article
-
- You have access
- Export citation
Computing separable isogenies in quasi-optimal time
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2015, pp. 198-216
-
- Article
-
- You have access
- Export citation
Construction of spline curves on smooth manifolds by action of Lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2015, pp. 217-230
-
- Article
-
- You have access
- Export citation
Piecewise Legendre spectral-collocation method for Volterra integro-differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 231-249
-
- Article
-
- You have access
- Export citation
Computing overconvergent forms for small primes
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 250-257
-
- Article
-
- You have access
- Export citation
Coleman integration for even-degree models of hyperelliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 258-265
-
- Article
-
- You have access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 308-322
-
- Article
-
- You have access
- Export citation
The maximal subgroups of
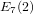 $E_{7}(2)$
$E_{7}(2)$
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 323-371
-
- Article
-
- You have access
- Export citation
Bespoke finite difference schemes that preserve multiple conservation laws
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2015, pp. 372-403
-
- Article
-
- You have access
- Export citation
Nilpotent-independent sets and estimation in matrix algebras
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2015, pp. 404-418
-
- Article
-
- You have access
- Export citation
Heuristics on pairing-friendly abelian varieties
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 419-443
-
- Article
-
- You have access
- Export citation
Virtual geometricity is rare
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2015, pp. 444-455
-
- Article
-
- You have access
- Export citation
Restricting unipotent characters in special orthogonal groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2015, pp. 456-488
-
- Article
-
- You have access
- Export citation
Schubert presentation of the cohomology ring of flag manifolds
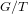 $G/T$
$G/T$
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 489-506
-
- Article
-
- You have access
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
The Runge–Kutta method in geometric multiplicative calculus
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 539-554
-
- Article
-
- You have access
- Export citation