A point in the plane is said to be a lattice point if it has integral coordinates. Given a set C of lattice points and two non-negative integers m and n, we are concerned with determining a set of m vertical and a set of n horizontal straight lines so that the number of intersections of these sets is maximal. In general, this problem is rather difficult, since we have to make simultaneous decisions about the positions of the vertical and horizontal straight lines. Our purpose here is to study a set of lattice points of the form (i, j) such that i, j, i + j and i − j are bounded by fixed integers. We shall show that, in this case, sequential decisions can be made about the two families of straight lines.

Let K be a quadratic imaginary number field with discriminant less than −4. For N either a number field or a finite extension of the p-adic field p, we let N denote the ring of integers of N. Moreover, if N is a number field then we write for the integral closure of [½] in N. For an integral ideal & of K we denote the ray classfield of K with conductor & by K(&). Once and for all we fix a choice of embedding of K into the complex numbers .

In this paper we prove several results concerning the complexity of a set relative to compact sets. We prove that for any Polish space X and Borel set B ⊆ X, if B is not , then there exists a compact zero-dimensional P ⊆ X such that p ∩ X is not . We also show that it is consistent with ZFC that, for any A ⊆ ωω, if for all compact K ⊆ ωωA ∩ K is , then A is . This generalizes to in place of assuming the consistency of some hypotheses involving determinacy. We give an alternative proof of the following theorem of Saint-Raymond. Suppose X and Y are compact metric spaces and f is a continuous surjection of X onto Y. Then, for any A ⊆ Y, A is in Y iff f−1(A) is in X. The non-trivial part of this result is to show that taking pre-images cannot reduce the Borel complexity of a set. The techniques we use are the definability of forcing and Wadge games.

Many of the basic concepts in this paper are defined in (2), and it will be useful to the reader if he is familiar with that paper. In it the concept of a loop transversal to a subgroup S of a group G is defined and discussed, where if G is a transitive permutation group and no explicit S is mentioned it is assumed that S is a point stabilizer. In (3) there appeared the following problem (P):

Let G be a transitive permutation group which is 2-closed.

(i) Is there a fixed-point-free transversal in G (i.e. to a point stabilizer)?

(ii) Is there a loop transversal in G?

Unfortunately a note was added in which it was falsely stated that the answer to both (i) and (ii) is yes.

For each integer m, Rasala [6] has shown how to list all the ordinary irreducible representations of the symmetric group n which have degree less than nm, provided that n is large enough, and in this note we shall prove similar results for the irreducible representations of n over an arbitrary field K. Our estimates are very crude, so although we recover Rasala's results, we get nowhere near his precise information on how large n has to be.

In his attempt to give the irreducible characters of the Weyl groups of type A, B and D, Mayer [3] found a unified theory using their common structure as reflection groups. In this paper, we give the characters of the complex imprimitive reflection groups. We are able to give an algorithm which allows us to calculate the irreducible components of the principal character of a ‘Weyl’ subgroup induced up to the whole group. This is a generalization of the algorithm given by Mayer.

In this paper, we study the structure of certain infinite-dimensional alternative algebras admitting an inner product and an involution. These algebras, called alter-native H*-algebras in the sequel, are the alternative analogues of the H*-algebras of Ambrose [1].

Every finitary algebra is, of course, a topological algebra in the discrete topology. On the other hand, a topological Boolean σ-algebra is indiscrete; sequences (0, 0, …, x, x,…) with join x converge to (0, 0,…) with join 0, so 0 is in {x}−, and similarly x is in {0}−. For lattices with infinite joins but only finite meets, such as topologies, the matter is more interesting.

In this paper we attempt to determine the mod p cohomology rings of the extra special p-groups for an odd prime p. Quillen has calculated the mod 2 case [8]. In our case, its structure seems to be very complicated [6]. It seems reasonable that we consider the variety defined by the cohomology ring of even degree according to Serre [11]. The main result of this paper (Theorem 5.3) gives a subalgebra of the cohomology ring such that the inclusion homomorphism induces a homeomorphism between the varieties.

In the previous papers in this series (see (5) and (6)) we used Brown-Peterson theory to obtain necessary conditions for the mod p cohomology of finite H-spaces to be U(M) algebras. In this paper we will use connective K-theory to strengthen the main results of (6). We should mention that we will be assuming a general knowledge of the previous two papers from this series. The definitions and notation from these papers will be used freely. (In particular, the reader is directed to § 2 of (5) for the definition of a U(M) algebra.)

In this paper we formulate and prove generalizations of a theorem of Lin [7]. Let X be a CW complex with base point x0. Define a free involution T on S∞×(X Λ X) by T (w, xΛy) = (−w, yΛx). The quadratic construction on X is the complex

This construction can be applied to spectra. A complete and thorough account will appear in the work on equivariant stable homotopy theory in preparation by L. G. Lewis, J. P. May, J. McLure and M. Steinberger. Some of the results are announced in [8].

In [2, 4, 5, 6, 7] Calabi, Barbosa and Chern showedthat there is a 2:1 correspondence between arbitrary pairs of full isotropic (terminology as in [8]) harmonic maps ±φ:M→S2m from a Riemann surface to a Euclidean sphere and full totally isotropic holomorphic maps f:M→2m from the surface to complex projective space. In this paper we show, very explicitly, how to construct a similar one-to-one correspondence when S2m is replaced by some other space forms of positive and negative curvatures with their standard (indefinite) metrics obtained by restricting a standard (indefinite) bilinear form on Euclidean space to the tangent spaces. We get over a difficulty encountered by Barbosa of dealing with the zeros of a certain wedge product by a technique adapted from [8]. The case of complex projective space forms (indefinite complex projective and complex hyperbolic spaces) will be considered in a separate paper. Some further developments in classification theorems are given by Eells and Wood [8], Rawnsley[14], [15] and Erdem and Wood [10].

In [8], Fialkow classified Einstein hypersurfaces in indefinite space forms, when the Weingarten endomorphism is diagonalizable. Recently, [13]–[15], Magid completed this work when such endomorphism is not diagonalizable. On the other hand, Smyth [17], classified complex Einstein hypersurfaces in complex space forms. Since Barros & Romero, [1], have made a systematic study of indefinite Kāhlerian manifolds, in particular, indefinite complex space forms, we investigate here complex Einstein non-degenerate hypersurfaces in indefinite complex space forms. In our case, we cannot always diagonalize the Weingarten endomorphism Aassociated to a unit normal field because it is a self-adjoint endomorphism in an indefinite metric vector space, but we prove that, if A is not diagonalizable, one has either A2 = 0 and A ≠ 0 or A2 = −γ2I, γε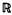. We obtain in Theorems 4.4 and 5.5 a full classification except in the case that the ambient space is flat and the Weingarten endomorphism A satisfies A2 = 0and A ≠0. Our classification is based on extending Smyth's results to show that, except in this last case, an Einstein hypersurface is locally symmetric. Using expressions for the curvature tensor to estimate the dimension of the isotropy group, together with Berger's list of symmetric spaces, [3], we then determine the possible Einstein hypersurfaces.

It is a classical result in the theory of special functions that Bessel functions are limits in an appropriate sense of Legendre polynomials. For example in (11), § 17.4, the following result is attributed to Heine:

such limiting formulae are also known for certain other special functions (cf. (1), (5)). Apart from their intrinsic interest, these formulae have been used in the theory of special functions to obtain product formulae, etc. for the limit function from those of the approximating sequence.

It is known, (see [7], theorem 4 or [8], corollary II, 10.1), that a positive generated, ordered Banach space X is order-isomorphic to l1 iff X has a Schauder basis which generates its positive cone X+ and X+ has a bounded base.

In this note we use the notion of the quasiasymptotic behaviour of distributions (introduced in [2]) in order to obtain a final value Abelian theorem for the distributional Stieltjes transformation. At the end of the note we give a few examples in which two different concepts of the asymptotic behaviour of distributions are compared.

For a system of partial differential equations, the existence of appropriate conservation laws is often a key ingredient in the investigation of its solutions and their properties. Conservation laws can be used in proving existence of solutions, decay and scattering properties, investigation of singularities, analysis of integrability properties of the system and so on. Representative applications, and more complete bibliographies on conservation laws, can be found in references [7], [8], [12], [19]. The more conservation laws known for a given system, the more tools available for the above investigations. Thus a complete classification of all conservation laws of a given system is of great interest. Not many physical systems have been subjected to such a complete analysis, but two examples can be found in [11] and [14]. The present paper arose from investigations ([15], [16]) into the conservation laws of the equations of elasticity.

In § 7 of [1] we described how a stochastic integral of non-commuting process cesan be constructed. This was achieved via a Doob-Meyer decomposition for the square of a self-adjoint L2-martingale. We introduced a ‘condition D'’ derived from the lsquo;class D’ of stochastic process theory, and showed that if the square of a self-adjoint L2-martingale satisfies this condition then it has a decomposition of the Doob-Meyer type. The purpose of this paper is to extend the results of § 7 of [1] and to introduce another construction of the stochastic integral that does not employ condition D.

The method to be described provides an alternative means of dealing with certain non-standard linear boundary-value problems. It is developed in several applications to the theory of gravity-capillary waves. The analysis is based on a variational formulation of the hydrodynamic problem, being motivated by and extending the original study by Benjamin and Scott [3].