Contents
Research Article
Shadow boundaries of typical convex bodies. measure properties
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
-
- Article
- Export citation
Scaling Hausdorff measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 325-333
-
- Article
- Export citation
The viscous flow through symmetric collapsible channels
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-181
-
- Article
- Export citation
Fractal series
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 334-348
-
- Article
- Export citation
On measure derivation in metric spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 349-358
-
- Article
- Export citation
Book Reviews
Book Reviews - B. J. Alder, Editor. Special Purpose Computers. Academic Press. 1988, 282 pp., $49.95. - D. R. Bland. Wave Theory and Applications. Clarendon Press. 1988, 317 pp., hardback £40, paperback £.15. - S.Caenepeel and F. Van Oystaeyen Brauer Groups and the Cohomology of Graded Rings. Marcel Dekker. 1988, 261 pp., 107.50. - G. F. Carrier and C. E. Pearson. Partial Differential Equations Theory and Technique. Academic Press. 1988, 340 pp., $39.95. - D. V. Chudnovsky and G. V. Chudnovsky Editors. Search Theory: Some Recent Developments. Marcel Dekker. 1989, 155 pp., $107.50. - R. Durrett. Lecture Notes on Particle Systems and Percolation. Wadsworth & Brooks/Cole. 1988, 335 pp., $39.95. - D. H. Griffel Linear Algebra and its Applications: Volume 1, A First Course. Ellis Horwood. 1989, 289 pp., £16.95. - S. P. Gudder. Quantum Probability. Academic Press. 1988, 316 pp., $49.50. - M. Hervé. Several Complex Variables: Local Theory, 2nd Edition. Oxford University Press. 1987, 148 pp., £8.95. - K. Ito and N. Ikeda, Editors. Probabilistic Methods in Mathematical Physics; Proceedings of the Katata and Kyoto Symposia: 1985. Academic Press.1988, 441 pp., $59.50. - G. Karpilovsky. Field theory: Classical Foundations and Multiplicative Groups. Marcel Dekker. 1988, 550 pp., $119.50. - P. Pelcé Editor. Dynamics of Curved Fronts. Academic Press. 1988, 514 pp., $69.50. - G. Sewell. The Numerical Solution of Ordinary and Partial Equations. Academic Press. 1988, 271 pp., $39.95. - J. S. Walker. Fourier Analysis. Oxford University Press. 1988, 440 pp., £40. - N. R. Wallach. Real Reductive Groups I. Academic Press. 1988, 412 pp., $59.95. - W. D. Wallis. Combinatorial Designs. Marcel Dekker. 1988, 323 pp., $107.50. - W. Wieslaw. Topological Fields. Marcel Dekker. 1988, 309 pp., $119.50.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-185
-
- Article
- Export citation
Front matter
MTK volume 36 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Book Reviews
Book Reviews - J. Aczél and J. Dhombres. Functional Equations in Several Variables. Cambridge University Press. 1989, 462 pp., £50. - R. S. Boyer and J. S. Moore. A Computational Logic Handbook. Academic Press. 1988, 408 pp., $39·95. - H. Brezis and J. L. Lions, Editors. Nonlinear Partial Differential Equations and Their Applications. Longman. 1988, 375 pp., £20. - K. S. Brown. Buildings. Springer. 1989, 215 pp., DM78. - E. Castillo. Extreme Value Theory in Engineering. Academic Press. 1988, 389 pp., $59·95. - B. Cipra. Misteaks… and How to Find Them Before the Teacher Does. 2nd Edition. Academic Press. 1989, 65 pp., $6·95. - P. M. Cohn. Algebra, Volume 2, 2nd edition. Wiley. 1989, 428 pp., £14·95. - M. S. P. Eastham. The Asymptotic Solution of Linear Differential Systems. Clarendon Press. 1989, 240 pp., £30. - D. E. Edmunds and W. D. Evans. Spectral Theory and Differential Operators. Clarendon Press. 1989, 574 pp., £25. - D. Guo and V. Lakshmikantham. Nonlinear Problems in Abstract Cones. Academic Press. 1988, 275 pp., $34·95. - C. W. Gardiner. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. 2nd Edition. Springer. 1985, 442 pp., DM99 - A. M. W. Glass and W. C. Holland, Editors. Lattice-Ordered Groups: Advances and Techniques. Kluwer Academic Publishers. 1989, 380 pp., £59. - D. H. Griffel. Linear Algebra and its Applications, Vol. 2. Ellis Horwood. 1989, 223 pp., £29·95. - K.-U. Grusa. Mathematical Analysis of Nonlinear Dynamic Processes and Their Applications. Longman. 1988, 450 pp., £25. - K. J. Hastings. Introduction to the Mathematics of Operations Research. Marcel Dekker. 1989, 424 pp., $119·50. - H. Hijikata, H. Hironaka, M. Maruyam, H. Matsumura, M. Miyanishi, T. Oda and K. Ueno, Editors. Algebraic Geometry and Commutative Algebra. Academic Press. 1988, Vol. I, 404 pp., Vol. II, 400 pp., $69 per volume. - M. Holt. Numerical Methods in Fluid Dynamics, 2nd Edition. Springer. 1984, 273 pp., DM74. - R. Peyret and T. D. Taylor. Computational Methods for Fluid Flow. Springer. 1986, 358 pp., DM86. - J. A. Huckaba. Commutative Rings with Zero-Divisors. Marcel Dekker. 1988, 216 pp., $95·95. - M. Kashiwara and T. Kawai, Editors. Albegraic Analysis: Papers Dedicated to Professor Mikio Sato On the Occasion of His 60th Birthday. Two Volumes. Academic Press. 1989, Vol. I 472 pp., Vol. II, 478 pp., $59·95 per volume. - F. Kirwan. An Introduction to Intersection Homology Theory. Longman. 1988, 169 pp., £15. - W. M. Kozlowski. Modular function spaces. Marcel Dekker. 1988, 252 pp., $107·50. - W. Kuich and A. Salomaa. Semirings, Automata, Languages. EATCS Monographs on Theoretical Computer Science. Springer. 1986, 374 pp., DM128. - G. R. Lindfield and J. E. T. Penny. Microcomputers in Numerical Analysis. Ellis Horwood. 1989, 453 pp., £39·95. - F. Liret and M. Zisman. Maths Tome 4, 5. Dunod. 1988, Tome 4, 249 pp., F95, Tome 5, 263 pp., F105. - J. J. Modi. Parallel Algorithms and Matrix Computation. Clarendon Press. 1988, 260 pp., £35. - D. Mumford. The Red Book of Varieties and Schemes. Lecture Notes in Mathematics, 1358. Springer. 1988, 309 pp., DM50. - H. Nagao and Y. Tsushima. Representations of Finite Groups. Academic Press. 1989, 424 pp., $70. - D. Passman. Infinite Crossed Products. Academic Press. 1989, 468 pp., $84·50. - M. Rapoport, N. Shappacher and P. Schneider, Editors. Beilinson's Conjectures on Special Values of L-Functions. Academic Press. 1988, 373 pp., $37·50. - L. RéDEI. Endliche p-Gruppen. Akadémiai Kiado, Budapest. 1989, 304 pp., £19·50. - H. Renelt. Elliptic Systems and Quasiconformal Mappings. Wiley. 1988, 146 pp., £14·95. - J. L. Richards. Mathematical Visions: The Pursuit of Geometry in Victorian England. Academic Press. 1988, 266 pp., $34·95. - P. Thomas, H. Robinson and J. Emms. Abstract Data Types. Clarendon Press. 1988, 256 pp., £12·50. - J. Traub, G. W. Wasilkowski and H. Wozniakowski. Information- Based Complexity. Academic Press. 1988, 523 pp., $64·50. - K. Varadarajan. The Finiteness Obstruction of C. T. C. Wall. Wiley. 1989, 194 pp., £33·75. - Wang Jianhua. The Theory of Games. Clarendon Press. 1988, 162 pp., £25. - N. A. Watson. Parabolic Equations on an Infinite Strip. Marcel Dekker. 1989, 256 pp., $119·50. - D. Zwillinger. Handbook of Differential Equations. Academic Press. 1988, 673 pp., $49·95.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-367
-
- Article
- Export citation
Index
Index to volume 36
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 368
-
- Article
- Export citation
Front matter
MTK volume 36 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
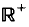 with θ(0)= 0 and let
with θ(0)= 0 and let 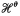 be the corresponding Hausdorff measure. We say that
be the corresponding Hausdorff measure. We say that 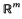 and
and 
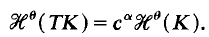
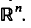 In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).
In Theorem 1 we give sufficient conditions for such series. Theorem 2 shows that each analytic function gives a different fractal series for each number in a certain open set. Theorem 3 gives the Hausdorff dimension of the associated sets to fractal series, under suitable conditions on the series. This theorem can be applied to some standard series in analysis, such as the binomial, exponential and trigonometrical complex series. The associated sets to geometrical complex series are selfsimilar sets previously studied by M. F. Barnsley from a different (dynamical) point of view (see refs. [5], [6]).