Contents
Research Article
Complete breakdown of an unsteady interactive boundary layer (over a surface distortion or in a liquid layer)
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 86-100
-
- Article
- Export citation
Spherical averages of Fourier transforms of measures with finite energy; dimensions of intersections and distance sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-228
-
- Article
- Export citation
Maximally symmetric polyhedral realizations of Dyck's regular map
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-236
-
- Article
- Export citation
Topological spaces with dense subspaces that are homeomorphic to complete metric spaces and the classification of C(K) Banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-107
-
- Article
- Export citation
A maximally symmetric polyhedron of genus 3 with 10 vertices
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 237-242
-
- Article
- Export citation
Book Reviews
Book Reviews - J. Aczél. A short course on Functional Equations. D. Reidel. 1987, 169 pp., £35. - L. V. Ahlfors. Lectures on quasiconformal mappings. Reprint of 1966 edition. Wadsworth. 1987, 146 pp., $24·95. - J. S. R. Chisholm and A. K. Common, Editors. Clifford Algebras and their applications in Mathematical Physics, NATO-ASI series. D. Reidel. 1986, 592 pp., £74·50. - L. Collatz. Differential Equations, an Introduction with Applications. J. Wiley & Sons. 1986, 372 pp., £11·95. - P. G. N. Digby and J. C. Gower. Ordination and Classification. Presses de l'Université de Montréal. 1986, 87 pp., Canadian $16. - D. G. Duffy. Solutions of Partial Differential Equations. J. Wiley & Sons. 1986, 542 pp., £23.85. - D. D. Holm, J. E. Marsden and T. S. Ratiu. Hamiltonian structure and Lyapunov stability for ideal continuum dynamics. Presses de l'Université de Montréal. 1986, 208 pp., Canadain $20. - A. Howard and P.-M. Wong, Editors. Contributions to several complex variables. Friedr. Vieweg & Sohn. 1986, 353 pp., £23·70. - J. A. John. Cyclic Design. Chapman & Hall. 1987, 232 pp, £16. - R. Kaya, P. Plaumann and K. Strambach, Editors. Rings and Geometry, NATO-ASI series. D. Reidel. 1985, 567 pp., £56·95. - G. G. Koch and P. B. Imrey. Analysis of Categorical Data. Presses de l'Université de Montréal. 1985, 288 pp., Canadian $22. - E. Kunz. Kähler Differentials. J. Wiley & Sons (for F. Vieweg & Sohn). 1986, 402 pp., £26·50. - W. Linde. Probability in Banach Spaces—Stable and Infinitely Divisible Distributions. J. Wiley & Sons. 1986, 195 pp., £16·50. - B. F. J. Manly. Multivariate Statistical Methods: A Primer. Chapman & Hall. 1986, 159 pp., hardback £15, paperback £6·95. - M. Minoux. Mathematical Programming. J. Wiley & Sons. 1986, 489 pp., £34.95. - J. Nečas. Introduction to the theory of non-linear elliptic equations. J. Wiley & Sons. 1986, 164 pp., £14·95. - H.-O. Peitgen and P. H. Richter. The Beauty of Fractals. Springer. 1986, 199 pp., DM78. - A. Pressley and G. Segal. Loop Groups. Oxford University Press. 1986, 318 pp., £40. - G.-C. Rota, Editor. Probability, Statistical Mechanics, and Number Theory: A volume dedicted to Mark Kac. Advances in Mathematics: supplementary studies, Vol. 9. Academic Press, 1986, 194 pp., £49.50. - J. D. H. Smith. Representation theory of infinite groups and finite quasigroups. Presses de l'Université de Montréal. 1986, 132 pp., Canadian $18. - E. J. Snell. Applied Statistics, a handbook of BMDP analyses. Chapman & Hall. 1987, 171 pp., paperback £7·95. - R. P. Stanley. Enumerative Combinatorics I. Wadsworth & Brooks/Cole. 1986, 306 pp. £42.95. - I. Stewart. The problems of mathematics. Oxford University Press. 1987, 257 pp., hard cover £17·50, paperback £5·95. - D. J. Struick, Editor. A source book in Mathematics, 1200–1800. Princeton University Press. 1986, 427 pp., £8·40. - M. Suzuki. Group Theory II. Springer. 1986, 621 pp., DM 268. - Ā Szendrei. Clones in universal algebra. Presses de l'Université de Montréal, 1986, 166 pp., Canadian $19. - E. C. Titchmarsh. The theory of the Riemann Zeta-function. 2nd Edition revised by D. R. Heath-Brown. Oxford University Press. 1986, 412 pp, £25. - P. Winternitz. Systéms dynamiques non-lineareaires: intégrabilité et comportement qualitatif. Presses de l'Université de Montréal. 1986, 339 pp., Canadian $30.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-113
-
- Article
- Export citation
Research Article
Internal characterization of fragmentable spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 243-257
-
- Article
- Export citation
Front matter
MTK volume 34 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Research Article
Radon-Nikodým compact spaces and fragmentability
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-281
-
- Article
- Export citation
Book Reviews
Book Reviews - I. Anderson. Combinatorics of Finite Sets. Oxford University Press. 1987, 250 pp., £22·50. - M. F. Atiyah et al., Editors. Vector bundles on algebraic varieties. Papers presented at the Bombay Colloquium, 1984. Oxford University Press. 1987, 555 pp., £22·50. - A. Borel et al. Algebraic D-modules. Academic Press. 1987, 355 pp., £25. - P. Blass and J. Lang, Editors. Zariski Surfaces and Differential Equations in Characteristic p > 0. M. Dekker. 1987, 441 pp., $95·50. - D. E. Cohen. Computability and Logic. Ellis Horwood. 1987, 243 pp., £36·50. - R. J. Daverman. Decomposition of Manifolds. Academic Press. 1986, 317 pp., £46. - G. Faltings, G. Wüstholz et al. Rational Points. Seminar Bonn/Wupperial 1983/84. F. Vieweg. 1986, 286 pp., £16·75. - W. Fulton and S. Lang. Riemann-Roch Algebra. Grundlehren d. Math. Wiss., 277. Springer. 1985, 203 pp., DM 158. - A. E. Gelfand, Editor. Contributions to the Theory and Applications of Statistics: A Volume in Honor of Herbert Solomon. Academic Press. 1987, 544 pp., $59·95. - L. J. Gerstein. Discrete Mathematics and Algebraic Structures. W. H. Freeman. 1987, 413 pp., £32·95. - F. Guaraldo, P. Macri and A. Tancredi. Topics on Real Analytic Spaces. Advanced Lectures in Mathematics. Vieweg. 1986, 163 pp., £16·40. - J. C. Jantzen. Representations of Algebraic Groups. Academic Press. 1987, 443 pp., $59.50. - G. S. Ladde, V. Lakshmikantham and B. G. Zhang. Oscillation Theory of Differential Equations with Deviating Arguments. M. Dekker. 1987, 308 pp., $107·50. - Leonardo Pisano Fibonacci. The Book of Squares. Academic Press. 1987, 124 pp., $19·95 or £17. - R. N. McKenzie, G. F. McNutty and W. F. Taylor. Algebras, Lattices, Varieties. Vol. 1. Wadsworth & Brooks/Cole. 1987, 361 pp., $44·95. - J. S. Milne. Arithmetic Duality Theorems. Academic Press. 1986, 421 pp., £32. - C. Năstăsescu and F. van Oystaeyen. Dimensions of Ring Theory. D. Reidel. 1987, 360 pp., £59. - J. Pöschel and E. Trubowitz. Inverse Spectral Theory. Academic Press. 1987, 192 pp., $29·95. - H.-J. Schmeisser and H. Triebel. Topics in Fourier Analysis and Function Spaces. J. Wiley. 1987, 300 pp., £23·95. - I. N. Stewart and D. O. Tall. Algebraic Number Theory. 2nd edition. Chapman & Hall. 1987, 262 pp., £9·95. - D. S. G. Stirling. Mathematical Analysis: a fundamental and straightforward approach. Ellis Horwood. 1987, 172 pp., £9·95. - D. Stoyan, W. S. Kendall and J. Mecke. Stochastic Geometry and its Applications. J. Wiley. 1987, 345 pp., £23.50. - R. A. Usmani. Applied Linear Algebra. Marcel Dekker. 1987, 258 pp., $47·50.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 282-286
-
- Article
- Export citation
Index
Index to Volume 34
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 287
-
- Article
- Export citation
Front matter
MTK volume 34 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
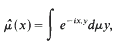
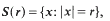
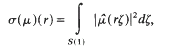
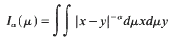
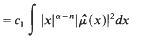
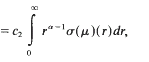
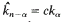 where
where 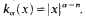 .
.