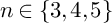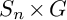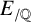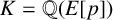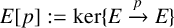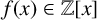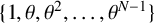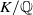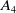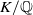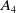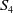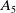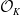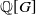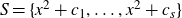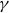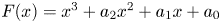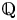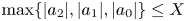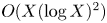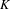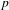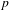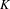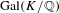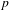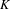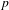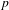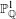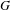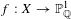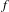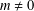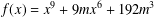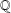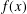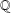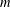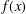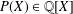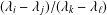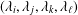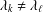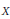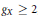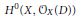38 results
ON MALLE’S CONJECTURE FOR THE PRODUCT OF SYMMETRIC AND NILPOTENT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-26
-
- Article
- Export citation
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 245-264
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
MONOGENIC QUARTIC POLYNOMIALS AND THEIR GALOIS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 244-259
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
MONOGENIC EVEN QUARTIC TRINOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 238-243
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Leopoldt-type theorems for non-abelian extensions of \mathbb{Q}
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
On metabelian 2-class field towers over \mathbb Z_2 -extensions of real quadratic fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 October 2021, pp. 795-805
- Print publication:
- September 2022
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
- Print publication:
- June 2021
-
- Article
- Export citation
A question for iterated Galois groups in arithmetic dynamics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 401-417
- Print publication:
- June 2021
-
- Article
- Export citation
The Trace Form Over Cyclic Number Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 947-969
- Print publication:
- August 2021
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
HEURISTICS FOR p-CLASS TOWERS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 26 December 2019, pp. 1429-1452
- Print publication:
- July 2021
-
- Article
- Export citation
DENSITY RESULTS FOR SPECIALIZATION SETS OF GALOIS COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 1455-1496
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
DISTRIBUTION OF GALOIS GROUPS OF MAXIMAL UNRAMIFIED 2-EXTENSIONS OVER IMAGINARY QUADRATIC FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 09 July 2018, pp. 166-187
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
AN INFINITE FAMILY OF NINTH DEGREE DIHEDRAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 47-53
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 185-190
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Faithfulness of Actions on Riemann-Roch Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 4 / 01 August 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-869
- Print publication:
- 01 August 2015
-
- Article
-
- You have access
- Export citation
Infinite Families of A4-Sextic Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-545
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation