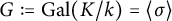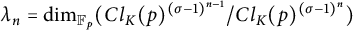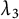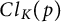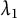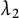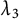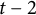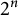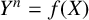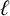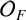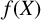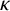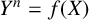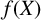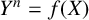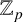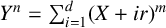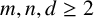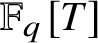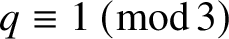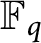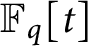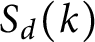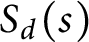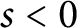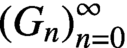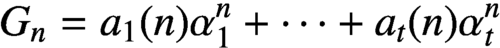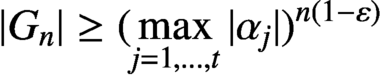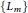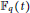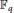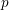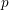34 results
Zagier–Hoffman’s Conjectures in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 October 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Infinite families of Artin–Schreier function fields with any prescribed class group rank
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1773-1794
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thakur’s basis conjecture for multiple zeta values in positive characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE EQUATIONS OF THE FORM
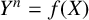 $Y^n=f(X)$ OVER FUNCTION FIELDS
$Y^n=f(X)$ OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 379-390
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonvanishing for cubic L-functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 October 2021, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of multizeta values over
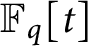 $\mathbb {F}_q[t]$
at negative integers
$\mathbb {F}_q[t]$
at negative integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 9-29
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 11-20
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
On square-free values of large polynomials over the rational function field
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 247-263
- Print publication:
- March 2021
-
- Article
- Export citation
DUALITY FOR COHOMOLOGY OF CURVES WITH COEFFICIENTS IN ABELIAN VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 42-149
- Print publication:
- December 2020
-
- Article
- Export citation
Weak Approximation for Points with Coordinates in Rank-one Subgroups of Global Function Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 878-890
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation
Regulators of an Infinite Family of the Simplest Quartic Function Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-594
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
Non-abelian Cohen–Lenstra heuristics over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 1372-1390
- Print publication:
- July 2017
-
- Article
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
The Distribution of the First Elementary Divisor of the Reductions of a Generic Drinfeld Module of Arbitrary Rank
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1326-1357
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation