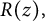 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 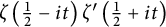 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
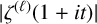 $|\zeta ^{(\ell )}(1+{i}t)|$
$|\zeta ^{(\ell )}(1+{i}t)|$
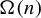 $\Omega (n)$
$\Omega (n)$