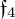 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND  $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
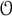 $\mathcal {O}$ for truncated current Lie algebras
$\mathcal {O}$ for truncated current Lie algebras
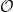 $\mathcal{O}$
$\mathcal{O}$
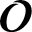 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS