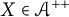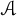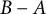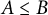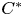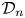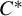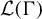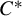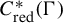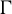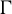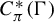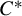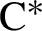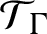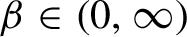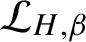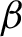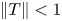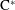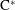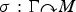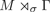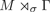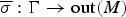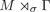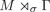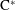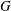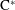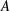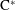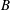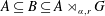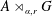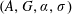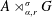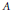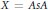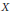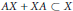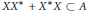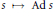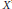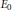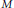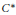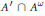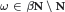38 results
Extending surjective maps preserving the norm of symmetric Kubo-Ando means
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 30 January 2025, pp. 1-10
-
- Article
- Export citation
Strongly outer actions of certain torsion-free amenable groups on the Razak–Jacelon algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Haagerup and Størmer's conjecture on pointwise inner automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 2480-2495
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
A classification of anomalous actions through model action absorption
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every symmetric Kubo–Ando connection has the order-determining property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 279-288
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
On conjugacy of subalgebras in graph C*-algebras. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1162-1182
-
- Article
- Export citation
On invariant subalgebras of group
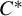 $C^*$ and von Neumann algebras
$C^*$ and von Neumann algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3341-3353
- Print publication:
- October 2023
-
- Article
- Export citation
The isomorphism problem for tensor algebras of multivariable dynamical systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KMS states for generalized gauge actions on
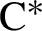 $\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 01 March 2022, pp. 1222-1238
- Print publication:
- April 2023
-
- Article
- Export citation
CENTRAL SEQUENCES IN SUBHOMOGENEOUS UNITAL C*-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 318-325
- Print publication:
- April 2021
-
- Article
- Export citation
On the von Neumann algebras associated to Yang–Baxter operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 1331-1354
- Print publication:
- August 2021
-
- Article
- Export citation
Corrigendum to: A Galois Correspondence for Reduced Crossed Products of Simple
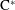 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 May 2019, pp. 557-562
- Print publication:
- April 2020
-
- Article
- Export citation
Fullness of crossed products of factors by discrete groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 2368-2378
- Print publication:
- October 2020
-
- Article
- Export citation
A Galois Correspondence for Reduced Crossed Products of Simple
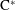 $\text{C}^{\ast }$-algebras by Discrete Groups
$\text{C}^{\ast }$-algebras by Discrete Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1103-1125
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A Note on Uniformly Bounded Cocycles into Finite Von Neumann Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 236-239
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
THE CLASSIFICATION PROBLEM FOR AUTOMORPHISMS OF C*-ALGEBRAS
-
- Journal:
- Bulletin of Symbolic Logic / Volume 21 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 15 January 2016, pp. 402-424
- Print publication:
- December 2015
-
- Article
- Export citation
Generalized Triple Homomorphisms and Derivations
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 783-807
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation
Partial ∗-Automorphisms, Normalizers, and Submodules in Monotone Complete C*-Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 6 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1144-1202
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Inner E0-Semigroups on Infinite Factors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 3 / 01 September 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-380
- Print publication:
- 01 September 2006
-
- Article
-
- You have access
- Export citation
Central Sequence Algebras of a Purely Infinite Simple C*-algebra
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 6 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1237-1258
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation