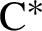 $\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
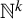 $\mathbb {N}^k$
-actions
$\mathbb {N}^k$
-actions
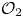 $\mathcal {O}_{2}$-absorption theorem for exact groups
$\mathcal {O}_{2}$-absorption theorem for exact groups