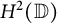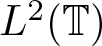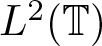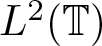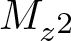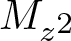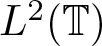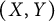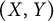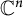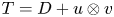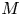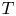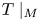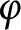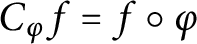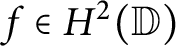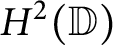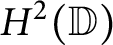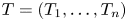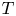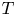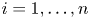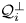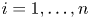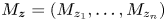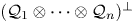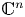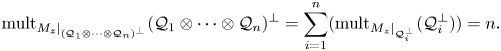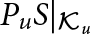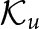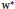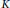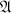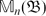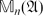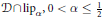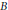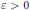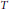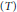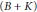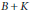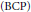47 results
Beurling type invariant subspaces on Hardy and Bergman spaces of the unit ball or polydisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 232-245
- Print publication:
- March 2025
-
- Article
- Export citation
Nearly invariant Brangesian subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 318-337
- Print publication:
- March 2025
-
- Article
- Export citation
Numerical invariants on twisted noncommutative polyballs: curvature and multiplicity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-54
-
- Article
-
- You have access
- HTML
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
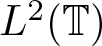 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
-
- You have access
- HTML
- Export citation
Nontrivial invariant subspaces of linear operator pencils
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1-8
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
General Toeplitz kernels and
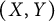 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
A note on cyclic vectors in Dirichlet-type spaces in the unit ball of
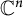 ${\mathbb C}^n$
${\mathbb C}^n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 886-902
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reducing subspaces for rank-one perturbations of normal operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 1391-1423
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness and stability of equilibrium states for random non-uniformly expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 27 July 2022, pp. 2589-2623
- Print publication:
- August 2023
-
- Article
- Export citation
Model spaces invariant under composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 204-217
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
The Dual of the Compressed Shift
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 98-111
- Print publication:
- March 2021
-
- Article
- Export citation
Free Multivariate w*-Semicrossed Products: Reflexivity and the Bicommutant Property
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1235
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
On the Uniqueness of Jordan Canonical Form Decompositions of Operators by K-theoretical Data
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-339
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
SUBMODULES OF COMMUTATIVE C*-ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 471-479
- Print publication:
- May 2014
-
- Article
-
- You have access
- Export citation
Closed Ideals in Some Algebras of Analytic Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 2 / 01 April 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-298
- Print publication:
- 01 April 2009
-
- Article
-
- You have access
- Export citation
The Invariant Subspace Problem for Non-Archimedean Banach Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 4 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 604-617
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
LIMITS OF HYPERCYCLIC AND SUPERCYCLIC OPERATOR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 367-376
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
On the Hyperinvariant Subspace Problem. IV
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 4 / 01 August 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-789
- Print publication:
- 01 August 2008
-
- Article
-
- You have access
- Export citation
Distance from Idempotents to Nilpotents
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 3 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 638-657
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation