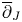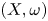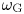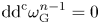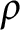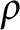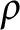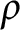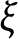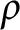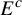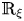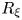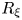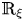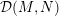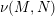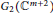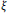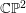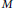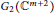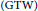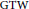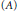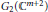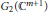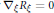48 results
On the Fatou theorem for ∂̄J-subsolutions in wedges
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 760-774
-
- Article
- Export citation
Singular Gauduchon metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 1314-1328
- Print publication:
- June 2022
-
- Article
- Export citation
Some characterizations of
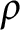 $\rho $
-Einstein solitons on Sasakian manifolds
$\rho $
-Einstein solitons on Sasakian manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 1036-1049
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic diffeomorphisms and Lagrangian contact structures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2583-2629
- Print publication:
- August 2022
-
- Article
- Export citation
Cyclic parallel structure Jacobi operator for real hypersurfaces in complex two-plane Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 12 August 2021, pp. 939-964
- Print publication:
- August 2022
-
- Article
- Export citation
Deformation spaces and normal forms around transversals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 697-732
- Print publication:
- April 2020
-
- Article
- Export citation
PARABOLIC COMPACTIFICATION OF HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 30 October 2019, pp. 1371-1408
- Print publication:
- July 2021
-
- Article
- Export citation
PLURIPOLAR SETS, REAL SUBMANIFOLDS AND PSEUDOHOLOMORPHIC DISCS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 270-288
- Print publication:
- October 2020
-
- Article
- Export citation
Lie Derivatives and Ricci Tensor on Real Hypersurfaces in Complex Two-plane Grassmannians
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 543-552
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
COMPLEX PRODUCT STRUCTURES ON HOM-LIE ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 March 2018, pp. 69-84
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
LEVI-UMBILICAL REAL HYPERSURFACES IN A COMPLEX SPACE FORM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 15 December 2016, pp. 99-112
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
A Classification of Three-dimensional Real Hypersurfaces in Non-flat Complex Space Forms in Terms of their Generalized Tanaka–Webster Lie Derivative
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 813-823
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Two-plane Grassmannians with Reeb Parallel Ricci Tensor in the GTW Connection
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-733
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Two-Plane Grassmannians with GTW Harmonic Curvature
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 835-845
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
QUASI-EINSTEIN CONTACT METRIC MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 569-577
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Two-Plane Grassmannians with Reeb Parallel Structure Jacobi Operator
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 821-833
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Projective Space Whose Structure Jacobi Operator is Lie 𝔻-parallel
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 306-316
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
On generalized Gauduchon metrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 733-753
-
- Article
-
- You have access
- Export citation
RICCI SOLITONS AND CONTACT METRIC MANIFOLDS
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 123-130
- Print publication:
- January 2013
-
- Article
-
- You have access
- Export citation
On Characterizations of Real Hypersurfaces in a Complex Space Form with η-Parallel Shape Operator
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-126
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation