24 results
The connective
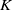 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 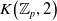 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 188-220
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
MORAVA K-THEORY AND FILTRATIONS BY POWERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1-77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BP-cohomology of projective Stiefel manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 679-701
- Print publication:
- April 2023
-
- Article
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
Holomorphic SCFTs with small index
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 573-601
- Print publication:
- April 2022
-
- Article
- Export citation
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation
MOTIVIC EULER CHARACTERISTICS AND WITT-VALUED CHARACTERISTIC CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 251-310
- Print publication:
- December 2019
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
Cohomological Approach to Class Field Theory in Arithmetic Topology
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 891-935
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
The ER(z)-cohomology of Bℤ/(2q) and ℂℙn
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-217
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
- Print publication:
- January 2020
-
- Article
- Export citation
The Weak b-principle: Mumford Conjecture
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-480
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
A generalization of Ohkawa’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 893-902
- Print publication:
- May 2014
-
- Article
- Export citation
Morava K-theory rings for the groups G38, …, G41 of order 32
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 06 December 2013, pp. 171-198
- Print publication:
- February 2014
-
- Article
- Export citation
Geometric K-homology with coefficients II: The Analytic Theory and Isomorphism
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 28 August 2013, pp. 235-256
- Print publication:
- October 2013
-
- Article
- Export citation
GEOMETRIC AND TOPOLOGICAL STRUCTURES RELATED TO M-BRANES II: TWISTED STRING AND STRINGC STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 93-108
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Towers of MU-Algebras and the Generalized Hopkins–Miller theorem
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 2 / September 2003
- Published online by Cambridge University Press:
- 26 September 2003, pp. 498-522
- Print publication:
- September 2003
-
- Article
- Export citation
Hecke Operations and the Adams E2-Term Based on Elliptic Cohomology
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-138
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation
A New Cohomological Criterion for the p-Nilpotence of Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 20-22
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation
The Hopf Ring for P(n)
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 5 / 01 October 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1044-1063
- Print publication:
- 01 October 1996
-
- Article
-
- You have access
- Export citation

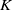
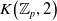
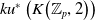
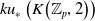
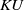
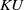
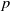
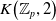
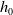
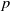
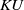
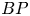
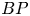
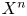
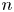
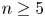
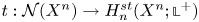
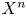
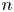
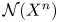
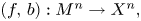
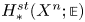
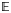
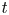
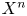
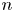
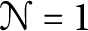
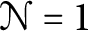


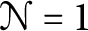
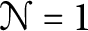
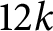
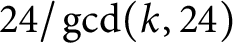
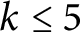
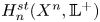
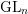
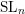
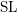
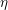
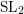
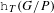
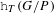

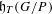
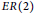
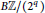
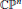
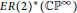
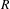
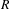
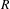
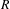
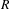
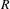
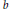
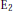
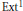
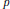
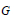
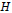
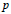
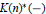
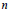
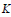
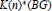
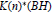
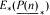 , the E-homology of the Ω-spectrum for P(n), is an E* free Hopf ring for E a complex oriented theory with I
, the E-homology of the Ω-spectrum for P(n), is an E* free Hopf ring for E a complex oriented theory with I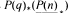 and
and 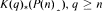 . The generators of the Hopf ring are those necessary for the stable result. The motivation for this paper is to show that P(n) satisfies all of the conditions for the machinery of unstable cohomology operations set up in [BJW95]. This can then be used to produce splittings analogous to those for BP done in [Wil75]
. The generators of the Hopf ring are those necessary for the stable result. The motivation for this paper is to show that P(n) satisfies all of the conditions for the machinery of unstable cohomology operations set up in [BJW95]. This can then be used to produce splittings analogous to those for BP done in [Wil75]