29 results
A Hamiltonian ∐n BO(n)-action, stratified Morse theory and the J-homomorphism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2005-2099
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
The Chromatic Fourier Transform
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher semiadditive algebraic K-theory and redshift
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 237-287
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the strict Picard spectrum of commutative ring spectra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1872-1897
- Print publication:
- September 2023
-
- Article
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISATIONS OF LODAY’S ASSEMBLY MAPS FOR LAWVERE’S ALGEBRAIC THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 811-837
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Topological models for stable motivic invariants of regular number rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 January 2022, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE TOM DIECK SPLITTING THEOREM IN EQUIVARIANT MOTIVIC HOMOTOPY THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1181-1250
- Print publication:
- May 2023
-
- Article
- Export citation
KHOVANOV SPECTRA FOR TANGLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1509-1580
- Print publication:
- July 2023
-
- Article
- Export citation
On
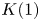 $K(1)$-local
$K(1)$-local 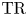 $\mathrm {TR}$
$\mathrm {TR}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1079-1119
- Print publication:
- May 2021
-
- Article
- Export citation
Stable homotopy refinement of quantum annular homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 710-769
- Print publication:
- April 2021
-
- Article
- Export citation
UNITARY FUNCTOR CALCULUS WITH REALITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 10 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
MULTIPLICATIVE PARAMETRIZED HOMOTOPY THEORY VIA SYMMETRIC SPECTRA IN RETRACTIVE SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 19 March 2020, e16
-
- Article
-
- You have access
- Open access
- Export citation
Freudenthal's theorem and spherical classes in H*QS0
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 323-341
-
- Article
- Export citation
On the Balmer spectrum for compact Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 39-76
- Print publication:
- January 2020
-
- Article
- Export citation
SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 May 2018, pp. 707-758
- Print publication:
- July 2019
-
- Article
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
- Print publication:
- January 2020
-
- Article
- Export citation
Ghosts and Strong Ghosts in the Stable Category
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 682-692
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
On the algebraic K-theory of truncated polynomial algebras in several variables
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 18 February 2014, pp. 57-81
- Print publication:
- February 2014
-
- Article
- Export citation

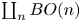
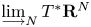
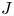
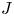
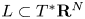
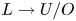
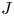
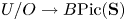
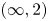
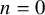
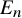
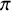
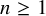
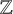
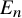
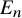
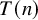
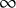
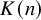
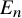

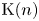
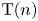
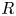
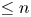
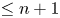
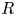
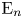
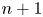
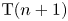
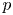
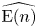
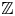
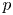
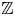
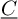
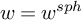
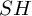
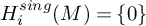
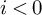
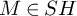

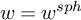
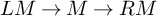
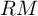
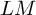
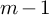
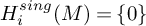
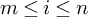
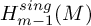

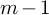
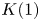
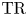
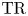
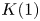
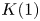
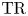
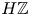
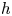
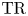
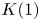
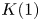
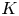
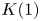
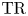
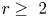
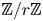
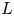
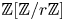
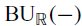 . The calculus produces a Taylor tower, the
. The calculus produces a Taylor tower, the 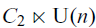 . We further give model categorical considerations, producing a zigzag of Quillen equivalences between spectra with an action of
. We further give model categorical considerations, producing a zigzag of Quillen equivalences between spectra with an action of 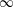
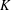
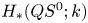
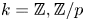

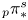
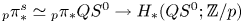

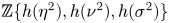

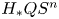
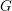
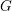
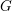
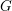
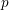
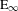
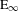
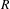
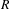
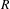
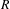
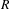
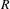
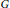

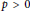
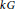
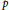


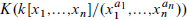 . This naturally leads to a new generalization of the big Witt vectors. If
. This naturally leads to a new generalization of the big Witt vectors. If 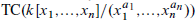 as the iterated homotopy cofiber of an
as the iterated homotopy cofiber of an 