20 results
PL homeomorphisms of surfaces and codimension 2 PL foliations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2684-2703
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion in classifying spaces of gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stable cohomology of self-equivalences of connected sums of products of spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The mod-p homology of the classifying spaces of certain gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1805-1817
- Print publication:
- December 2023
-
- Article
- Export citation
Decoupling Decorations on Moduli Spaces of Manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 163-198
- Print publication:
- January 2023
-
- Article
- Export citation
ABELIAN CYCLES IN THE HOMOLOGY OF THE TORELLI GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1703-1726
- Print publication:
- July 2023
-
- Article
- Export citation
EULER CLASSES: SIX-FUNCTORS FORMALISM, DUALITIES, INTEGRALITY AND LINEAR SUBSPACES OF COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 16 July 2021, pp. 681-746
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Braid groups, mapping class groups and their homology with twisted coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 249-266
- Print publication:
- March 2022
-
- Article
- Export citation
TAUTOLOGICAL RINGS AND STABILISATION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 17 March 2021, pp. 231-242
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation
Non-torsion non-algebraic classes in the Brown–Peterson tower
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 October 2020, pp. 113-132
- Print publication:
- July 2021
-
- Article
- Export citation
ON THE COHOMOLOGY OF TORELLI GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 April 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
Classifying spaces for étale algebras with generators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 854-874
- Print publication:
- June 2021
-
- Article
- Export citation
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
Classifying spaces for commutativity of low-dimensional Lie groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 433-478
- Print publication:
- November 2020
-
- Article
- Export citation
Tautological rings for high-dimensional manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 851-866
- Print publication:
- April 2017
-
- Article
- Export citation
Morava K-theory rings for the groups G38, …, G41 of order 32
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 06 December 2013, pp. 171-198
- Print publication:
- February 2014
-
- Article
- Export citation
ON THE COHOMOLOGY OF CONFIGURATION SPACES ON SURFACES
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 25 September 2003, pp. 477-492
- Print publication:
- October 2003
-
- Article
- Export citation
Nilpotency and triviality of mod p Morita-Mumford classes of mapping class groups of surfaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 165 / March 2002
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-22
- Print publication:
- March 2002
-
- Article
-
- You have access
- Export citation
Stiefel-Whitney Classes of a Symmetric Bilinear Form — A Formula of Serre
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 218-222
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation






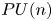
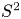

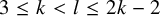
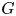


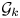
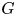
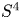
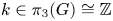
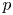
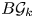
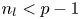
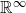
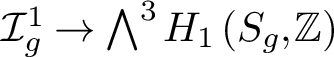
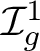
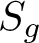
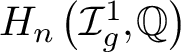
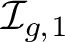
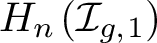
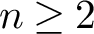
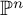
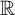
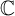
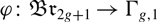
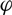
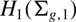
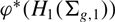
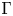
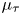
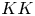
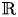
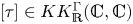
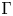
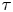
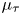
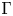
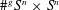
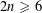
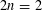
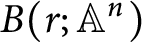
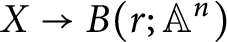
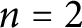
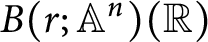
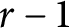
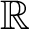
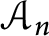
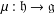
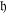
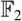
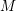
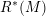
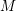
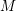
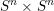

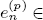
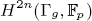 of the mapping class group Γ
of the mapping class group Γ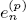 is nilpotent if
is nilpotent if 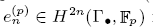 is proved to be nontrivial and not nilpotent if
is proved to be nontrivial and not nilpotent if  is the separable closure of K, we have a continuous homomorphism π : Ga(
is the separable closure of K, we have a continuous homomorphism π : Ga(