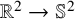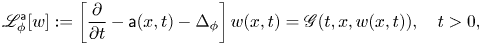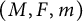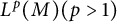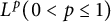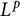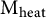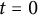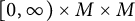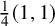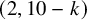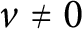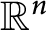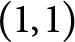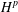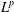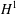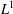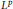24 results
Continuous in time bubble decomposition for the harmonic map heat flow
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness of
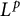 $L^p$ subsolutions to the heat equation on Finsler measure spaces
$L^p$ subsolutions to the heat equation on Finsler measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 166-175
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Heat kernel asymptotics for real powers of Laplacians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 January 2023, pp. 367-393
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp endpoint estimates for some operators associated with the Laplacian with drift in Euclidean space
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 1278-1304
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Non-collapsing in homogeneity greater than one via a two-point method for a special case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1627-1635
- Print publication:
- December 2019
-
- Article
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
Pinning Effect on Current-Induced Domain Wall Motion in Nanostrip
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 837-851
- Print publication:
- November 2017
-
- Article
- Export citation
HARDY SPACES ON METRIC MEASURE SPACES WITH GENERALIZED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 162-194
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
An index theorem for end-periodic operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 399-444
- Print publication:
- February 2016
-
- Article
- Export citation
QUASI RIESZ TRANSFORMS, HARDY SPACES AND GENERALISED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 10 August 2015, pp. 508-510
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Musielak–Orlicz Hardy Spaces Associated with Divergence Form Elliptic Operators Without Weight Assumptions
-
- Journal:
- Nagoya Mathematical Journal / Volume 216 / 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 71-110
- Print publication:
- 2014
-
- Article
-
- You have access
- Export citation
On Durbin's Series for the Density of First Passage Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-722
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
An approximation for the inverse first passage time problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 264-275
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
FOURTH ORDER GEOMETRIC EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 November 2010, pp. 523-524
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON THE BLOW-UP OF THE NON-LOCAL THERMISTOR PROBLEM
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 17 May 2007, pp. 389-409
-
- Article
-
- You have access
- Export citation
SHARP GRADIENT ESTIMATE AND YAU'S LIOUVILLE THEOREM FOR THE HEAT EQUATION ON NONCOMPACT MANIFOLDS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 6 / December 2006
- Published online by Cambridge University Press:
- 19 December 2006, pp. 1045-1053
- Print publication:
- December 2006
-
- Article
- Export citation
Reverse Hypercontractivity for Subharmonic Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 3 / 01 June 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 506-534
- Print publication:
- 01 June 2005
-
- Article
-
- You have access
- Export citation
HEAT CONTENT AND A HARDY INEQUALITY FOR COMPLETE RIEMANNIAN MANIFOLDS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 24 August 2004, pp. 577-586
- Print publication:
- September 2004
-
- Article
- Export citation