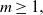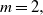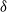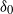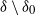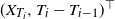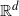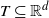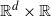93 results
EXPLORING OUT-OF-SAMPLE PREDICTION AND SPATIAL DEPENDENCY FOR COMPLEX BIG DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
Persistence of spectral projections for stochastic operators on large tensor products
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-14
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sojourn functionals for spatiotemporal Gaussian random fields with long memory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 148-165
- Print publication:
- March 2023
-
- Article
- Export citation
Reciprocal properties of random fields on undirected graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 781-796
- Print publication:
- September 2023
-
- Article
- Export citation
Inheritance of strong mixing and weak dependence under renewal sampling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 435-451
- Print publication:
- June 2023
-
- Article
- Export citation
ON ASYMPTOTIC PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 518-521
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
ON MULTIFRACTIONALITY OF SPHERICAL RANDOM FIELDS WITH COSMOLOGICAL APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 90-118
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A deep look into the dagum family of isotropic covariance functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
- Print publication:
- December 2022
-
- Article
- Export citation
STOCHASTIC MODELLING AND STATISTICAL ANALYSIS OF SPATIAL AND LONG-RANGE DEPENDENT DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 170-173
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Long range dependence of heavy-tailed random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 569-593
- Print publication:
- September 2021
-
- Article
- Export citation
Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 42-67
- Print publication:
- March 2021
-
- Article
- Export citation
ON STATISTICAL PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 18 September 2020, pp. 338-340
- Print publication:
- April 2021
-
- Article
-
- You have access
- Export citation
ON ASYMPTOTICS OF FUNCTIONALS OF RANDOM FIELDS WITH LONG-RANGE DEPENDENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 518-521
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
STATISTICAL ANALYSIS OF LONG-RANGE DEPENDENT RANDOM PROCESSES AND FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 345-347
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
THEORY AND STATISTICS OF LONG-RANGE DEPENDENT RANDOM PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 339-341
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
SOME LIMIT THEOREMS OF DELAYED AVERAGES FOR COUNTABLE NONHOMOGENEOUS MARKOV CHAINS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 24 September 2019, pp. 297-315
-
- Article
- Export citation
Cramér type moderate deviations for random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 223-245
- Print publication:
- March 2019
-
- Article
- Export citation
Exact moderate and large deviations for linear random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 431-449
- Print publication:
- June 2018
-
- Article
- Export citation
A large sample test for the length of memory of stationary symmetric stable random fields via nonsingular ℤd-actions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 179-195
- Print publication:
- March 2018
-
- Article
- Export citation
Percolation results for the continuum random cluster model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 231-244
- Print publication:
- March 2018
-
- Article
- Export citation