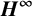 ${\boldsymbol H}^{\boldsymbol{\infty}}$
MAPS
${\boldsymbol H}^{\boldsymbol{\infty}}$
MAPS
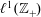 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
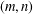 $(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
$(m,n)$-JORDAN DERIVATIONS OF RINGS AND BANACH ALGEBRAS
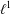 $\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
$\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS