20 results
7 - Climate Change and Marine Protected Areas Network
-
- Book:
- Regulating the Sea
- Published online:
- 15 December 2022
- Print publication:
- 22 December 2022, pp 128-144
-
- Chapter
- Export citation

Regulating the Sea
- A Socio-Legal Analysis of English Marine Protected Areas
-
- Published online:
- 15 December 2022
- Print publication:
- 22 December 2022
VARIATION ON A THEME BY KISELEV AND NAZAROV: HÖLDER ESTIMATES FOR NONLOCAL TRANSPORT-DIFFUSION, ALONG A NON-DIVERGENCE-FREE BMO FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1651-1675
- Print publication:
- September 2022
-
- Article
- Export citation
A NEW LINEAR AND CONSERVATIVE FINITE DIFFERENCE SCHEME FOR THE GROSS–PITAEVSKII EQUATION WITH ANGULAR MOMENTUM ROTATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 08 April 2019, pp. 204-232
-
- Article
-
- You have access
- Export citation
Conservation Introductions for Biodiversity Adaptation under Climate Change
-
- Journal:
- Transnational Environmental Law / Volume 7 / Issue 2 / July 2018
- Published online by Cambridge University Press:
- 11 January 2018, pp. 323-345
-
- Article
- Export citation
Symmetry-invariant conservation laws of partial differential equations†
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 March 2017, pp. 78-117
-
- Article
- Export citation
Runge-Kutta Discontinuous Galerkin Method with a Simple and Compact Hermite WENO Limiter
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 944-969
- Print publication:
- April 2016
-
- Article
- Export citation
High Order Energy-Preserving Method of the “Good” Boussinesq Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 15 February 2016, pp. 111-122
- Print publication:
- February 2016
-
- Article
- Export citation
A New Family of High Order Unstructured MOOD and ADER Finite Volume Schemes for Multidimensional Systems of Hyperbolic Conservation Laws
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 718-763
- Print publication:
- September 2014
-
- Article
- Export citation
Numerical Solutions of Coupled Nonlinear Schrödinger Equations by Orthogonal Spline Collocation Method
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 5 / November 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1392-1416
- Print publication:
- November 2012
-
- Article
- Export citation
AN EQUAL-AREA METHOD FOR SCALAR CONSERVATION LAWS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 28 May 2012, pp. 156-170
-
- Article
-
- You have access
- Export citation
EXPLICIT SERIES SOLUTION OF A CLOSURE MODEL FOR THE VON KÁRMÁN–HOWARTH EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 05 September 2011, pp. 179-202
-
- Article
-
- You have access
- Export citation
A convergence result for finite volume schemeson Riemannian manifolds
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 43 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 12 June 2009, pp. 929-955
- Print publication:
- September 2009
-
- Article
- Export citation
Convergence of implicit Finite Volume methods for scalar conservation laws with discontinuous flux function
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 04 July 2008, pp. 699-727
- Print publication:
- September 2008
-
- Article
- Export citation
The minimum entropy principle for compressible fluid flows in a nozzle with discontinuous cross-section
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 03 April 2008, pp. 425-442
- Print publication:
- May 2008
-
- Article
- Export citation
Number-Conserving Reversible Cellular Automata and Their Computation-Universality
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 3 / May 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 239-258
- Print publication:
- May 2001
-
- Article
- Export citation
Convergence of finite difference schemes for viscousand inviscid conservation laws with rough coefficients
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 35 / Issue 2 / March 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 239-269
- Print publication:
- March 2001
-
- Article
- Export citation
On the controllability of the Burger equation
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 3 / 1998
- Published online by Cambridge University Press:
- 15 August 2002, pp. 83-95
- Print publication:
- 1998
-
- Article
- Export citation
A flow conservation law for surface processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 13-28
- Print publication:
- March 1996
-
- Article
- Export citation
Pseudo-conservation laws in cyclic-service systems
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 949-964
- Print publication:
- December 1987
-
- Article
- Export citation

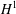
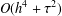

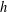
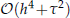 and the stability of the scheme are proved. Conservation properties are shown in both theory and practice. Extensive numerical experiments are presented to validate the numerical study under consideration.
and the stability of the scheme are proved. Conservation properties are shown in both theory and practice. Extensive numerical experiments are presented to validate the numerical study under consideration.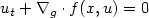
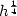
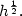
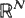 and
and 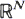 . The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field
. The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field 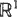 this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.
this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.