Refine search
Actions for selected content:
12 results
Omega results for the error term in the square-free divisor problem for square-full integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1011-1028
- Print publication:
- December 2024
-
- Article
- Export citation
Generalized divisor functions in arithmetic progressions: II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 28-56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
- Print publication:
- April 2022
-
- Article
- Export citation
DISTRIBUTION OF THE DIVISOR FUNCTION AT CONSECUTIVE INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 09 September 2020, pp. 244-247
- Print publication:
- April 2021
-
- Article
- Export citation
A SHIFTED CONVOLUTION SUM OF
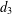 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 26 September 2019, pp. 401-414
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
NOTE ON THE NUMBER OF DIVISORS OF REDUCIBLE QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1-9
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
IMPROVING AN INEQUALITY FOR THE DIVISOR FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 374-381
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
SHIFTED CONVOLUTION SUM OF
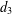 $d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
$d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 195-204
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Averages of shifted convolutions of d3(n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 551-576
-
- Article
-
- You have access
- Export citation
CONVOLUTION SUMS INVOLVING THE DIVISOR FUNCTION
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 3 / October 2004
- Published online by Cambridge University Press:
- 09 November 2004, pp. 561-572
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Class Number of a Real Quadratic Field of ERD-Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-96
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
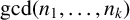

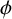
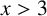
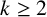
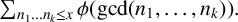
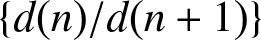
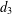
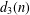


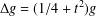
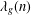

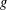
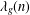


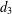
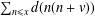

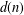

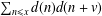
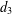
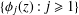
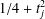
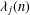

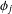
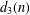
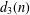
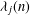
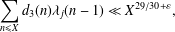
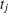

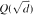 in general, but applied to greatest advantage when
in general, but applied to greatest advantage when 