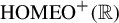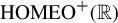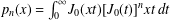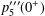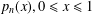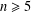47 results
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONDITIONS FOR RECURRENCE AND TRANSIENCE FOR TIME-INHOMOGENEOUS BIRTH-AND-DEATH PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 393-402
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Strong Shannon–McMillan–Breiman’s theorem for locally compact groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 1274-1279
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of the first positions of uniform parking functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1201-1218
- Print publication:
- December 2023
-
- Article
- Export citation
Reflection principle for finite-velocity random motions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 479-492
- Print publication:
- June 2023
-
- Article
- Export citation
On random walks and switched random walks on homogeneous spaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 398-421
-
- Article
- Export citation
Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 764-830
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A stochastic process on a network with connections to Laplacian systems of equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 January 2022, pp. 254-278
- Print publication:
- March 2022
-
- Article
- Export citation
Diffusion profile embedding as a basis for graph vertex similarity
-
- Journal:
- Network Science / Volume 9 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 October 2021, pp. 328-353
-
- Article
-
- You have access
- Open access
- Export citation
On uniqueness of invariant measures for random walks on {\textup {HOMEO}}^+(\mathbb R)
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 29 April 2021, pp. 2207-2238
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Local limit theorems in relatively hyperbolic groups I: rough estimates
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 1926-1966
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Gradient and Harnack-type estimates for PageRank
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 03 September 2020, pp. S4-S22
-
- Article
- Export citation
Out-of-equilibrium random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 772-797
- Print publication:
- September 2020
-
- Article
- Export citation

The Missing Two-Thirds of Evolutionary Theory
-
- Published online:
- 25 February 2020
- Print publication:
- 26 March 2020
-
- Element
- Export citation
ON BORWEIN’S CONJECTURES FOR PLANAR UNIFORM RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 09 October 2019, pp. 392-411
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Clustering ensembles of social networks
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 15 April 2019, pp. 141-159
-
- Article
- Export citation
Kesten’s theorem for uniformly recurrent subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 2778-2787
- Print publication:
- October 2020
-
- Article
- Export citation
On–off intermittency and chaotic walks
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1805-1842
- Print publication:
- July 2020
-
- Article
-
- You have access
- Open access
- Export citation
THE FRIENDSHIP PARADOX FOR WEIGHTED AND DIRECTED NETWORKS
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 33 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 136-145
-
- Article
- Export citation