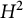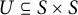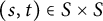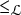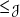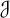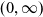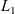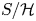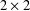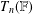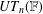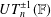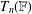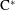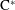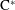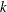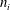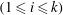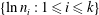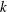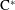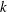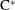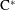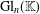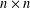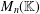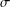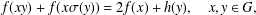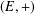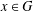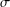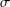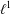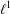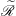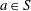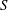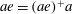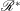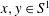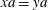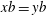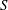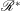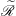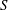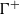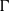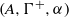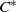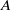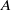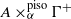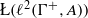46 results
Embedding of some classes of operators into strongly continuous semigroups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 219-231
- Print publication:
- March 2025
-
- Article
- Export citation
On minimal ideals in pseudo-finite semigroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 2007-2037
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fragmentation equation with size diffusion: Well posedness and long-term behaviour
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 December 2021, pp. 1083-1116
-
- Article
- Export citation
Semigroups whose right ideals are finitely generated
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 01 October 2021, pp. 848-883
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SEPARABILITY FINITENESS CONDITIONS IN SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 402-430
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
- Print publication:
- December 2021
-
- Article
- Export citation
A construction of subshifts and a class of semigroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 881-905
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
Amenability and Fixed Point Properties of Semitopological Semigroups in Modular Vector Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 692-704
- Print publication:
- September 2020
-
- Article
- Export citation
THE FINITE BASIS PROBLEM FOR INVOLUTION SEMIGROUPS OF TRIANGULAR 2\times 2 MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 88-104
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Boundary Quotient \text{C}^{\ast }-algebras of Products of Odometers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 183-212
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
ON THE HYPERSTABILITY OF A PEXIDERISED \unicode[STIX]{x1D70E}-QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 459-470
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Well-posedness and regularity of linear hyperbolic systems with dynamic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 1047-1080
- Print publication:
- October 2016
-
- Article
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
The Growth Bound for Strongly Continuous Semigroups on Fréchet Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 23 November 2015, pp. 801-810
-
- Article
- Export citation
A SUFFICIENT CONDITION UNDER WHICH A SEMIGROUP IS NONFINITELY BASED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 454-466
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
HOMOMORPHISMS OF \ell ^{1}-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 115-122
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON WEAKLY AMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 404-417
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
THE PARTIAL-ISOMETRIC CROSSED PRODUCTS BY SEMIGROUPS OF ENDOMORPHISMS AS FULL CORNERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 145-166
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
Abelian Semigroups of Matrices on ℂn and Hypercyclicity
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 05 September 2013, pp. 323-338
-
- Article
-
- You have access
- Export citation