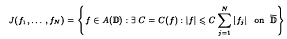Research Article
On the one-dimensional nonlinear elastohydrodynamic lubrication
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-372
-
- Article
-
- You have access
- Export citation
Free Lie algebra and lambda-ring structure
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 373-382
-
- Article
-
- You have access
- Export citation
Well-posedness of determining the source term of an elliptic equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 383-398
-
- Article
-
- You have access
- Export citation
Induced representations twisted by cocycles
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-404
-
- Article
-
- You have access
- Export citation
Approximation of a quasilinear elliptic equation with nonlinear boundary condition
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-424
-
- Article
-
- You have access
- Export citation
Convergence of approximate solutions of a quasilinear partial differential equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-433
-
- Article
-
- You have access
- Export citation
Use of the rabinowitsch polynomial to determine the class groups of a real quadratic field
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-443
-
- Article
-
- You have access
- Export citation
On projective lift and orbit spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 445-449
-
- Article
-
- You have access
- Export citation
On Hau's lemma
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-458
-
- Article
-
- You have access
- Export citation
Groups covered by finitely many nilpotent subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-464
-
- Article
-
- You have access
- Export citation
Linear parabolic equations with venttsel initial boundary conditions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-479
-
- Article
-
- You have access
- Export citation
Regularisations of convex functions and slicewise suprema
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-499
-
- Article
-
- You have access
- Export citation
Existence of entire solutions for some elliptic systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 501-519
-
- Article
-
- You have access
- Export citation
Finitely generated ideals in the disk algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-528
-
- Article
-
- You have access
- Export citation
Author Index, Volume 41 (1990) – 50 (1994)
Bulletin of the Australian Mathematical Society Author Index, Volume 41 (1990) – 50 (1994)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 529-559
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 50 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 50 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

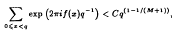
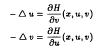
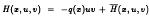 with
with 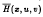 (
(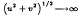 .
.