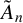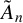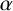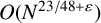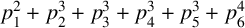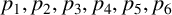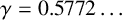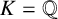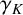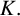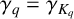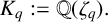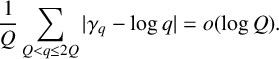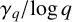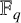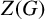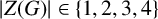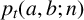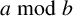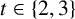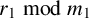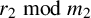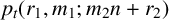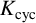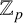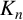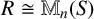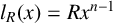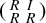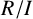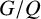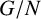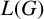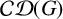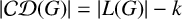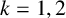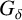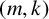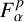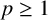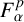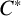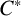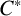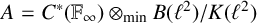Research Article
SPACINGS BETWEEN SELECTED PRIME DIVISORS OF AN INTEGER
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 403-415
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CANONICAL DECOMPOSITION AND QUIVER REPRESENTATIONS OF TYPE \tilde {A}_n OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2022, pp. 250-260
-
- Article
- Export citation
ON THE WARING–GOLDBACH PROBLEM FOR ONE SQUARE, FOUR CUBES AND ONE BIQUADRATE
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 416-431
-
- Article
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMOOTHNESS IN PENCILS OF HYPERSURFACES OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. 85-94
-
- Article
- Export citation
FINITE GROUPS WITH ABNORMAL MINIMAL NONNILPOTENT SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. 261-270
-
- Article
- Export citation
ON THE NUMBER OF 2-HOOKS AND 3-HOOKS OF INTEGER PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2022, pp. 432-439
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REMARKS ON HILBERT’S TENTH PROBLEM AND THE IWASAWA THEORY OF ELLIPTIC CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2022, pp. 440-450
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME PRODUCTS OF SUBGROUPS AND VANISHING CONJUGACY CLASS SIZES
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2022, pp. 271-275
-
- Article
- Export citation
A CHARACTERISATION OF MATRIX RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2022, pp. 95-101
-
- Article
- Export citation
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. 102-111
-
- Article
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH LARGE CHERMAK–DELGADO LATTICES
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. 451-455
-
- Article
- Export citation
OSCILLATION OF IMPULSIVE LINEAR DIFFERENTIAL EQUATIONS WITH DISCONTINUOUS SOLUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 05 May 2022, pp. 112-124
-
- Article
- Export citation
ERDŐS–LIOUVILLE SETS
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2022, pp. 284-289
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS IN WHICH ALL LARGE SUBGROUPS HAVE BOUNDED NEAR DEFECT
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2022, pp. 456-463
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HANKEL MEASURES FOR FOCK SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 290-295
-
- Article
- Export citation
ON \mathbf{\mathit{C}}^{*} -ALGEBRAS WHICH DETECT NUCLEARITY
- Part of:
-
- Published online by Cambridge University Press:
- 05 May 2022, pp. 125-133
-
- Article
- Export citation
A DOMAIN WITH NONPLURISUBHARMONIC d-BALANCED SQUEEZING FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. 464-470
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
-
- Article
- Export citation