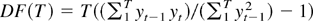Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 3
INSTRUMENTAL VARIABLE QUANTILE REGRESSION WITH MISCLASSIFICATION
-
- Published online by Cambridge University Press:
- 13 March 2020, pp. 169-204
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 3
The Equivalence of the Boothe-MacKinnon and the Hausman Specification Tests in the Context of Panel Data
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 409-410
-
- Article
- Export citation
- Cited by 3
THE ET INTERVIEW: PROFESSOR GARY CHAMBERLAIN
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2021, pp. 1-26
-
- Article
- Export citation
- Cited by 3
QUANTILOGRAMS UNDER STRONG DEPENDENCE
-
- Published online by Cambridge University Press:
- 30 August 2019, pp. 457-487
-
- Article
- Export citation
- Cited by 3
A NOVEL APPROACH TO PREDICTIVE ACCURACY TESTING IN NESTED ENVIRONMENTS
-
- Published online by Cambridge University Press:
- 17 May 2023, pp. 35-78
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 3
Time Series Analysis in Pooled Cross-Sections
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 331-349
-
- Article
- Export citation
- Cited by 3
THE DICKEY–FULLER TEST FOR EXPONENTIAL RANDOM WALKS
-
- Published online by Cambridge University Press:
- 04 August 2003, pp. 865-877
-
- Article
- Export citation
- Cited by 3
IMPROVED AND EXTENDED END-OF-SAMPLE INSTABILITY TESTS USING A FEASIBLE QUASI-GENERALIZED LEAST SQUARES PROCEDURE
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 994-1031
-
- Article
- Export citation
- Cited by 3
JOINT TIME-SERIES AND CROSS-SECTION LIMIT THEORY UNDER MIXINGALE ASSUMPTIONS
-
- Published online by Cambridge University Press:
- 11 August 2020, pp. 942-958
-
- Article
- Export citation
- Cited by 3
ESTIMATION OF COINTEGRATING VECTORS WITH TIME SERIES MEASURED AT DIFFERENT PERIODICITY
-
- Published online by Cambridge University Press:
- 19 July 2005, pp. 735-756
-
- Article
- Export citation
- Cited by 3
IDENTIFICATION IN DISCRETE MARKOV DECISION MODELS
-
- Published online by Cambridge University Press:
- 23 September 2014, pp. 521-538
-
- Article
- Export citation
- Cited by 3
SEMIPARAMETRIC INDEPENDENCE TESTING FOR TIME SERIES OF COUNTS AND THE ROLE OF THE SUPPORT
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 1111-1145
-
- Article
- Export citation
- Cited by 3
OBITUARY: G.S. Maddala, 1933–1999
-
- Published online by Cambridge University Press:
- 01 August 1999, pp. 639-641
-
- Article
-
- You have access
- Export citation
- Cited by 3
ROBUST INFERENCE IN STRUCTURAL VECTOR AUTOREGRESSIONS WITH LONG-RUN RESTRICTIONS
-
- Published online by Cambridge University Press:
- 05 March 2019, pp. 86-121
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 3
ON DISCRETE SAMPLING OF TIME-VARYING CONTINUOUS-TIME SYSTEMS
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 985-994
-
- Article
- Export citation
- Cited by 3
SIMULTANEOUS CONFIDENCE BANDS FOR CONDITIONAL VALUE-AT-RISK AND EXPECTED SHORTFALL
-
- Published online by Cambridge University Press:
- 03 August 2022, pp. 1009-1043
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 3
COMMON STOCHASTIC TRENDS AND AGGREGATION IN HETEROGENEOUS PANELS
-
- Published online by Cambridge University Press:
- 06 December 2006, pp. 89-105
-
- Article
- Export citation
- Cited by 3
A Comparison of Variance ComponentsEstimators Using Balanced Versus UnbalancedData
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 425-427
-
- Article
- Export citation
- Cited by 3
RENORMING VOLATILITIES IN A FAMILY OF GARCH MODELS
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 1370-1382
-
- Article
- Export citation
- Cited by 3
Handbook of Econometrics, vol. 4Robert F. Engle and Daniel L. McFadden, Editors Elsevier Science B. V., 1994
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 119-132
-
- Article
- Export citation