Contents
Research Article
Constraints on dynamics preserving certain hyperbolic sets
-
- Published online by Cambridge University Press:
- 26 May 2010, pp. 719-739
-
- Article
- Export citation
Gibbs-like measure for spectrum of a class of quasi-crystals
-
- Published online by Cambridge University Press:
- 14 January 2011, pp. 1669-1695
-
- Article
- Export citation
Embedding ℤk-actions in cubical shifts and ℤk-symbolic extensions
-
- Published online by Cambridge University Press:
- 26 March 2010, pp. 383-403
-
- Article
- Export citation
A topological lens for a measure-preserving system
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 49-75
-
- Article
- Export citation
An invariant of finitary codes with finite expected square root coding length
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 77-90
-
- Article
- Export citation
Spatial models of Boolean actions and groups of isometries
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 405-421
-
- Article
- Export citation
Reducibility of quasiperiodic cocycles in linear Lie groups
-
- Published online by Cambridge University Press:
- 10 May 2010, pp. 741-769
-
- Article
- Export citation
Ideal tilings and symbolic dynamics for negatively curved surfaces
-
- Published online by Cambridge University Press:
- 14 September 2011, pp. 1697-1726
-
- Article
- Export citation
Approximating invariant densities of metastable systems
-
- Published online by Cambridge University Press:
- 02 September 2010, pp. 1345-1361
-
- Article
- Export citation
On quasi-compact Markov nets
-
- Published online by Cambridge University Press:
- 20 July 2010, pp. 1081-1094
-
- Article
- Export citation
On a type III1 Bernoulli shift
-
- Published online by Cambridge University Press:
- 21 January 2011, pp. 1727-1743
-
- Article
- Export citation
Non-expansive directions for ℤ2 actions
-
- Published online by Cambridge University Press:
- 24 March 2010, pp. 91-112
-
- Article
- Export citation
Thermodynamic formalism for a family of non-uniformly hyperbolic horseshoes and the unstable Jacobian
-
- Published online by Cambridge University Press:
- 17 March 2010, pp. 423-447
-
- Article
- Export citation
Extreme value theory and return time statistics for dispersing billiard maps and flows, Lozi maps and Lorenz-like maps
-
- Published online by Cambridge University Press:
- 30 June 2011, pp. 1363-1390
-
- Article
- Export citation
Schmidt’s game, fractals, and orbits of toral endomorphisms
-
- Published online by Cambridge University Press:
- 05 August 2010, pp. 1095-1107
-
- Article
- Export citation
Multiple recurrence for two commuting transformations
-
- Published online by Cambridge University Press:
- 23 June 2010, pp. 771-792
-
- Article
- Export citation
An example of a non-uniquely ergodic lamination
-
- Published online by Cambridge University Press:
- 26 May 2010, pp. 449-457
-
- Article
- Export citation
Rigidity and mapping class group for abstract tiling spaces
-
- Published online by Cambridge University Press:
- 14 March 2011, pp. 1745-1783
-
- Article
- Export citation
Hénon-like maps with arbitrary stationary combinatorics
-
- Published online by Cambridge University Press:
- 09 March 2011, pp. 1391-1443
-
- Article
- Export citation
Nil–Bohr sets of integers
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 113-142
-
- Article
-
- You have access
- Export citation

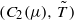 defined on the space of twofold couplings of
defined on the space of twofold couplings of 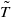 . Some of our main results are as follows: (i)
. Some of our main results are as follows: (i) 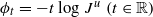 and the class of non-uniformly hyperbolic horseshoes which was introduced in Rios [Unfolding homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies.
and the class of non-uniformly hyperbolic horseshoes which was introduced in Rios [Unfolding homoclinic tangencies inside horseshoes: hyperbolicity, fractal dimensions and persistent tangencies. 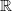 . We give the exact equations of the two asymptotes to the graph of 𝒫(
. We give the exact equations of the two asymptotes to the graph of 𝒫(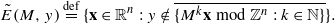
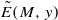 has full Hausdorff dimension. In this paper we strengthen this result, extending it to arbitrary
has full Hausdorff dimension. In this paper we strengthen this result, extending it to arbitrary 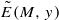 and their generalizations always intersect with ‘sufficiently regular’ fractal subsets of ℝ
and their generalizations always intersect with ‘sufficiently regular’ fractal subsets of ℝ