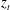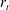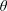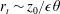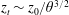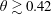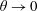Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 3
Steady two-dimensional viscous flow in a jet
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 49-63
-
- Article
- Export citation
- Cited by 3
Mixing induced by oscillatory stratified flow past a right-circular cylinder
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 1-21
-
- Article
- Export citation
- Cited by 3
On moderate injection into a separated supersonic boundary layer, with reattachment
-
- Published online by Cambridge University Press:
- 19 April 2006, pp. 115-132
-
- Article
- Export citation
- Cited by 3
On the stability of boundary-layer flow over a spring-mounted piston
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 59-73
-
- Article
- Export citation
- Cited by 3
Interfacial instabilities in plane Poiseuille flow of two stratified viscoelastic fluids with heat transfer. Part 1. Evolution equation and stability analysis
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 241-265
-
- Article
- Export citation
- Cited by 3
On the mixing of a low Reynolds number biological jet with a quiescent outer bathing solution
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 159-175
-
- Article
- Export citation
- Cited by 3
The interaction of a fibre tangle with an airflow
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 561-580
-
- Article
- Export citation
- Cited by 3
Inertial collapse of a gas bubble in a shear flow near a rigid wall
-
- Published online by Cambridge University Press:
- 28 January 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Long-wave instabilities of sloping stratified exchange flows
-
- Published online by Cambridge University Press:
- 02 April 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Magnetohydrodynamic Flows and Turbulence: a report on the Fourth Beer-Sheva Seminar
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 461-476
-
- Article
- Export citation
- Cited by 3
Wave effects on the hydroelastic response of a surface-piercing hydrofoil. Part 1. Fully wetted and ventilated flows
-
- Published online by Cambridge University Press:
- 22 May 2023, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Secondary generation of breaking internal waves in confined basins by gravity currents
-
- Published online by Cambridge University Press:
- 30 April 2021, A49
-
- Article
- Export citation
- Cited by 3
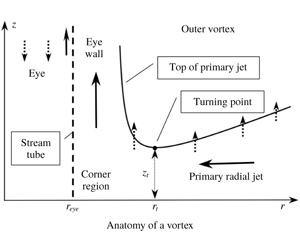
Turbulent boundary-layer flow beneath a vortex. Part 2. Power-law swirl
-
- Published online by Cambridge University Press:
- 03 April 2020, A17
-
- Article
- Export citation
- Cited by 3
Local effects of gravity on foams
-
- Published online by Cambridge University Press:
- 15 November 2013, pp. 1-18
-
- Article
- Export citation
- Cited by 3
A Hamiltonian Dysthe equation for deep-water gravity waves with constant vorticity
-
- Published online by Cambridge University Press:
- 07 October 2022, A50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
On the zero helicity condition for quantum vortex defects
-
- Published online by Cambridge University Press:
- 16 May 2023, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Acoustic emission due to the interaction between shock and instability waves in two-dimensional supersonic jet flows
-
- Published online by Cambridge University Press:
- 06 January 2023, A35
-
- Article
- Export citation
- Cited by 3
Optimal growth of counter-rotating vortex pairs interacting with walls
-
- Published online by Cambridge University Press:
- 06 October 2020, A10
-
- Article
- Export citation
- Cited by 3
Inverse transfer of magnetic helicity in direct numerical simulations of compressible isothermal turbulence: scaling laws
-
- Published online by Cambridge University Press:
- 11 March 2021, A23
-
- Article
- Export citation
- Cited by 3
On the stability of inhomogeneous fluids under acoustic fields
-
- Published online by Cambridge University Press:
- 30 May 2023, A23
-
- Article
- Export citation