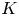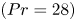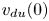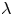Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 4
Interaction between a rough bed and an adjacent smooth bed in open-channel flow
-
- Published online by Cambridge University Press:
- 22 August 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 4
Bubble rise in a Hele-Shaw cell: bridging the gap between viscous and inertial regimes
-
- Published online by Cambridge University Press:
- 18 May 2022, R3
-
- Article
- Export citation
- Cited by 4
Explicit Dirichlet–Neumann operator for water waves
-
- Published online by Cambridge University Press:
- 24 October 2022, A33
-
- Article
- Export citation
- Cited by 3
Mixing induced by oscillatory stratified flow past a right-circular cylinder
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 1-21
-
- Article
- Export citation
- Cited by 3
A laboratory study of internal gravity waves incident upon slopes with varying surface roughness
-
- Published online by Cambridge University Press:
- 20 May 2022, A26
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 3
Turbulent energy transfers in physical and scale spaces at dissipative length scales
-
- Published online by Cambridge University Press:
- 06 December 2023, A27
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 3
Coating flow on a rotating cylinder in the presence of an irrotational airflow with circulation
-
- Published online by Cambridge University Press:
- 09 December 2021, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
On the zero helicity condition for quantum vortex defects
-
- Published online by Cambridge University Press:
- 16 May 2023, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
High-Prandtl-number thermocapillary liquid bridges with dynamically deformed interface: effect of an axial gas flow on the linear stability
-
- Published online by Cambridge University Press:
- 08 January 2024, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
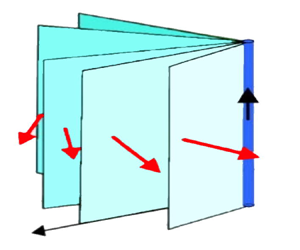
Flow regimes in a melting system composed of binary fluid: transition from penetrative convection to diffusion
-
- Published online by Cambridge University Press:
- 25 October 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Investigation of Lagrangian Areas of Minimal Stretching (LAMS) in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 04 September 2023, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Regular reflection to Mach reflection (RR–MR) transition in short wedges
-
- Published online by Cambridge University Press:
- 31 October 2024, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Inertial collapse of a gas bubble in a shear flow near a rigid wall
-
- Published online by Cambridge University Press:
- 28 January 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Three-dimensional aspects of nonlinear stratified flow over topography near the hydrostatic limit
-
- Published online by Cambridge University Press:
- 13 February 2001, pp. 81-105
-
- Article
- Export citation
- Cited by 3
Sub-representative elementary volume homogenization of flow in porous media with isolated embedded fractures
-
- Published online by Cambridge University Press:
- 26 August 2020, A20
-
- Article
- Export citation
- Cited by 3
George Batchelor: a personal tribute, ten years on
-
- Published online by Cambridge University Press:
- 04 November 2010, pp. 2-7
-
- Article
- Export citation
- Cited by 3
Fluttering-induced flow in a closed chamber
-
- Published online by Cambridge University Press:
- 28 November 2023, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Effects of highly pulsatile inflow frequency on surface-mounted bluff body wakes
-
- Published online by Cambridge University Press:
- 13 October 2020, A29
-
- Article
- Export citation
- Cited by 3
Solitary waves perturbed by a broad sill. Part 1. Propagation across the sill
-
- Published online by Cambridge University Press:
- 18 October 2019, pp. 916-934
-
- Article
- Export citation
- Cited by 3
Canonical wall-bounded flows: how do they differ?
-
- Published online by Cambridge University Press:
- 09 June 2015, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation