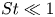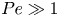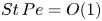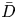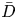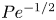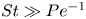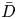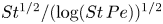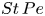Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
The role of polymer molecular weight distribution in drag-reducing turbulent flows
-
- Published online by Cambridge University Press:
- 14 March 2025, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Prandtl–Batchelor theorem for flows with quasiperiodic time dependence
-
- Published online by Cambridge University Press:
- 07 January 2019, R1
-
- Article
- Export citation
- Cited by 2
Stable three-dimensional vortex families consistent with Jovian observations including the Great Red Spot
-
- Published online by Cambridge University Press:
- 12 April 2024, A61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Görtler-number-based scaling of boundary-layer transition on rotating cones in axial inflow
-
- Published online by Cambridge University Press:
- 16 May 2024, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Bendocapillary instability of liquid in a flexible-walled channel
-
- Published online by Cambridge University Press:
- 16 January 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Non-normal stability analysis of a shear current under surface gravity waves
-
- Published online by Cambridge University Press:
- 31 July 2008, pp. 49-58
-
- Article
- Export citation
- Cited by 2
Particle capture by expanding droplets: effects of inner diffusion
-
- Published online by Cambridge University Press:
- 13 September 2022, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Numerical solutions of the unsteady Fanno model for compressible pipe flow
-
- Published online by Cambridge University Press:
- 02 May 2007, pp. 493-507
-
- Article
- Export citation
- Cited by 2
Nearly symmetric and nearly baroclinic instabilities in the presence of diffusivity. Part 2. Mode structures and energetics
-
- Published online by Cambridge University Press:
- 03 February 2004, pp. 283-312
-
- Article
- Export citation
- Cited by 2
Theory of the Eulerian tail in the spectra of atmospheric and oceanic internal gravity waves
-
- Published online by Cambridge University Press:
- 28 April 2003, p. 412
-
- Article
-
- You have access
- Export citation
- Cited by 2
Influences of small-scale shear instability on passive-scalar mixing in a shear-free turbulent front
-
- Published online by Cambridge University Press:
- 02 April 2025, A20
-
- Article
- Export citation
- Cited by 2
New scaling laws for turbulent Poiseuille flow with wall transpiration – ERRATUM
-
- Published online by Cambridge University Press:
- 30 June 2014, p. 746
-
- Article
-
- You have access
- Export citation
- Cited by 2
Bubble capture by a propeller
-
- Published online by Cambridge University Press:
- 20 July 2006, pp. 311-320
-
- Article
- Export citation
- Cited by 2
Local vortex line topology and geometry in turbulence
-
- Published online by Cambridge University Press:
- 05 August 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
General variational model reduction applied to incompressible viscous flows
-
- Published online by Cambridge University Press:
- 25 December 2008, pp. 31-50
-
- Article
- Export citation
- Cited by 2
Topological bifurcations in the transition from two single vortices to a pair and a single vortex in the periodic wake behind an oscillating cylinder
-
- Published online by Cambridge University Press:
- 08 April 2022, A22
-
- Article
- Export citation
- Cited by 2
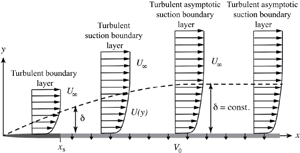
Laboratory realization of an asymptotic wall flow
-
- Published online by Cambridge University Press:
- 06 May 2021, F1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 2
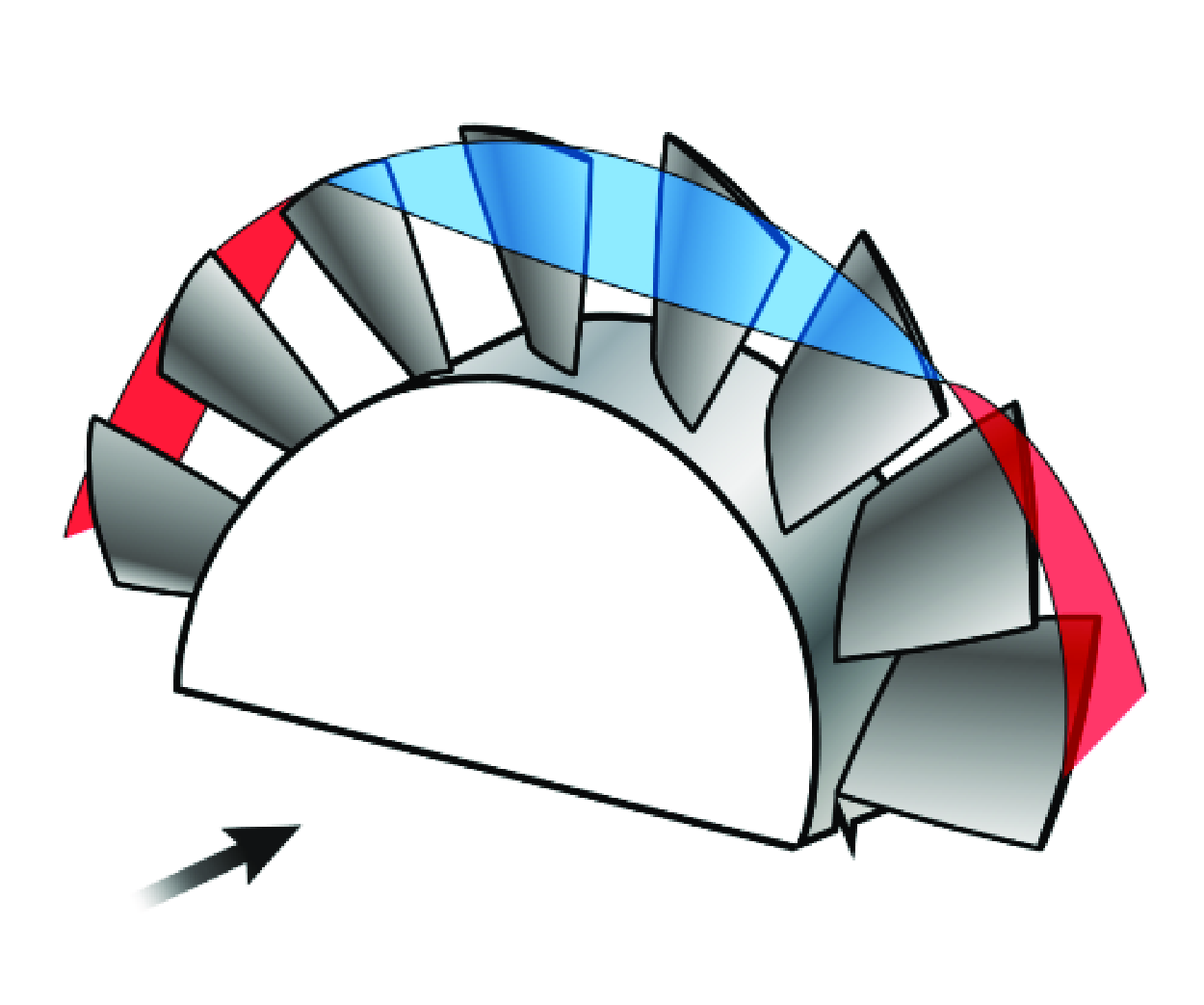
Acoustic resonance in annular cascades in the presence of background mean flow
-
- Published online by Cambridge University Press:
- 03 March 2025, A7
-
- Article
- Export citation
- Cited by 2
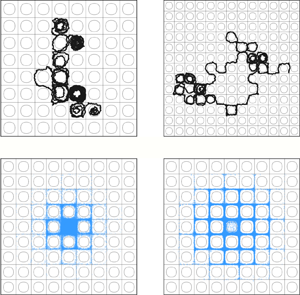
Dispersion of inertial particles in cellular flows in the small-Stokes, large-Péclet regime
-
- Published online by Cambridge University Press:
- 17 September 2020, A2
-
- Article
- Export citation
- Cited by 2
Clustering of buoyant tracer in quasi-geostrophic coherent structures
-
- Published online by Cambridge University Press:
- 14 January 2025, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation