Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
Slippery bounces
-
- Published online by Cambridge University Press:
- 26 May 2020, F1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 2
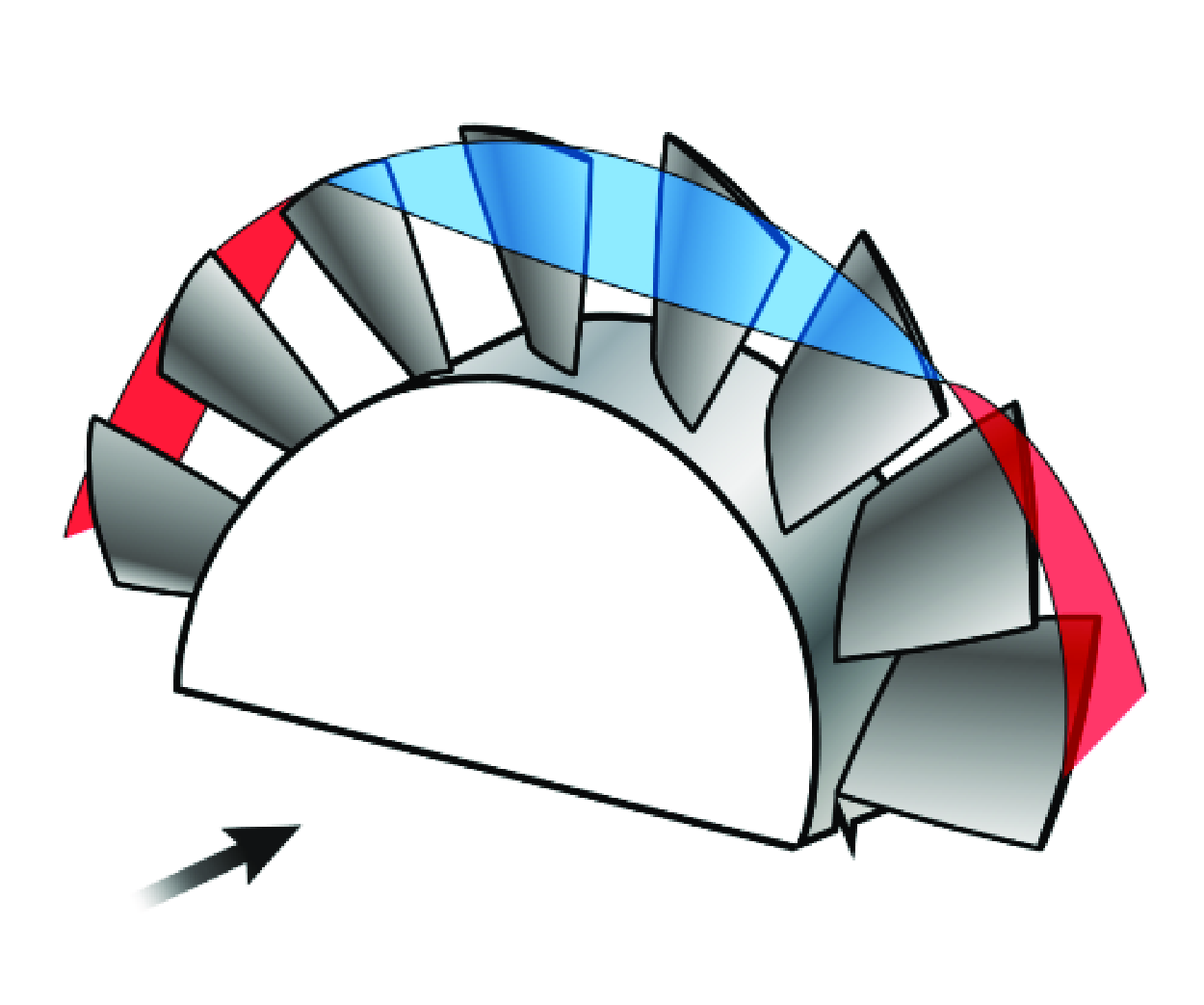
Acoustic resonance in annular cascades in the presence of background mean flow
-
- Published online by Cambridge University Press:
- 03 March 2025, A7
-
- Article
- Export citation
- Cited by 2
Immersed body motion: near-bottom added mass effects
-
- Published online by Cambridge University Press:
- 30 March 2022, A18
-
- Article
- Export citation
- Cited by 2
Viscosity, surface tension and gravity effects on acoustic reflection and refraction
-
- Published online by Cambridge University Press:
- 14 December 2018, pp. 822-836
-
- Article
- Export citation
- Cited by 2
Global stability analysis of elastic aircraft in edge-of-the-envelope flow
-
- Published online by Cambridge University Press:
- 12 July 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
General variational model reduction applied to incompressible viscous flows
-
- Published online by Cambridge University Press:
- 25 December 2008, pp. 31-50
-
- Article
- Export citation
- Cited by 2
Linear stability analysis of oblique Couette–Poiseuille flows
-
- Published online by Cambridge University Press:
- 29 October 2024, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Machine-learning wall-model large-eddy simulation accounting for isotropic roughness under local equilibrium
-
- Published online by Cambridge University Press:
- 14 March 2025, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
The effects of vertical mixing on nonlinear Kelvin waves
-
- Published online by Cambridge University Press:
- 28 September 2020, A22
-
- Article
- Export citation
- Cited by 2
Three-dimensional bursting process and turbulent coherent structure within scour holes at various development stages around a cylindrical structure
-
- Published online by Cambridge University Press:
- 17 October 2024, A61
-
- Article
- Export citation
- Cited by 2
Direct calculation of the eddy viscosity operator in turbulent channel flow at Reτ = 180
-
- Published online by Cambridge University Press:
- 31 October 2024, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Theoretical modelling of non-equilibrium reaction–diffusion of rarefied gas on a wall with microscale roughness
-
- Published online by Cambridge University Press:
- 20 June 2023, A21
-
- Article
- Export citation
- Cited by 2
Mathematical modelling of impurity deposition during evaporation of dirty liquid in a porous material
-
- Published online by Cambridge University Press:
- 10 May 2024, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Potential vorticity redistribution by localised transient forcing in the shallow-water model
-
- Published online by Cambridge University Press:
- 03 August 2018, pp. 199-225
-
- Article
- Export citation
- Cited by 2
Modelling the response of a vibrating-element density meter in a two-phase mixture
-
- Published online by Cambridge University Press:
- 10 June 1997, pp. 343-360
-
- Article
- Export citation
- Cited by 2
Bendocapillary instability of liquid in a flexible-walled channel
-
- Published online by Cambridge University Press:
- 16 January 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Effect of fluid motions on finite spheres released in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 23 April 2024, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Clustering of buoyant tracer in quasi-geostrophic coherent structures
-
- Published online by Cambridge University Press:
- 14 January 2025, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 2
Topology of shallow-water waves on a rotating sphere
-
- Published online by Cambridge University Press:
- 24 January 2025, A35
-
- Article
- Export citation
- Cited by 2
Viscous irrotational analysis of the deformation and break-up time of a bubble or drop in uniaxial straining flow*
-
- Published online by Cambridge University Press:
- 09 November 2011, pp. 390-421
-
- Article
- Export citation



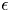




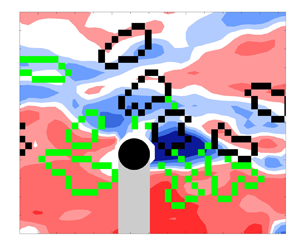
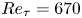
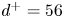





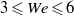 , predictions from viscous potential flow shows good agreement with the results from the Navier–Stokes equations for the bubble break-up time, whereas for larger
, predictions from viscous potential flow shows good agreement with the results from the Navier–Stokes equations for the bubble break-up time, whereas for larger 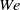 , the former underpredicts the results given by the latter. When viscosity is included, larger break-up times are predicted with respect to the inviscid case for the same
, the former underpredicts the results given by the latter. When viscosity is included, larger break-up times are predicted with respect to the inviscid case for the same 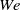 . For the drop, and considering moderate Reynolds numbers,
. For the drop, and considering moderate Reynolds numbers, 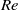 , increasing the viscous effects of the irrotational motion produces large, elongated drops that take longer to break up in comparison with results for inviscid fluids. For larger
, increasing the viscous effects of the irrotational motion produces large, elongated drops that take longer to break up in comparison with results for inviscid fluids. For larger 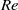 , it comes as a surprise that break-up times smaller than the inviscid limit are obtained. Unfortunately, results from numerical analyses of the incompressible, unsteady Navier–Stokes equations for the case of a drop have not been presented in the literature, to the best of the authors’ knowledge; hence, comparison with the viscous irrotational analysis is not possible.
, it comes as a surprise that break-up times smaller than the inviscid limit are obtained. Unfortunately, results from numerical analyses of the incompressible, unsteady Navier–Stokes equations for the case of a drop have not been presented in the literature, to the best of the authors’ knowledge; hence, comparison with the viscous irrotational analysis is not possible.