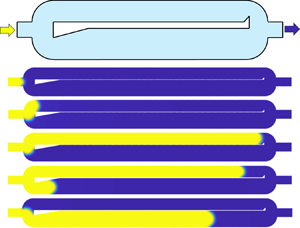
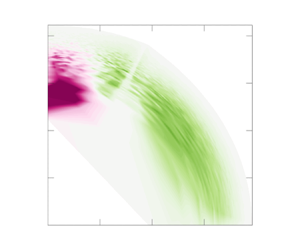
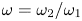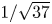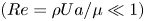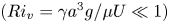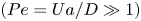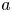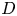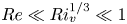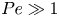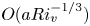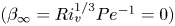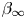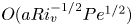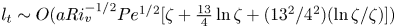doi:10.1017/jfm.2024.1105 Dandekar et al. Splash on a liquid pool: coupled cavity-sheet unsteady dynamics
Contents
JFM Papers
Scaling and dynamics of vortex lock-in for circular cylinders in an oscillating flow
-
- Published online by Cambridge University Press:
- 07 January 2025, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Restricted Euler dynamics in free-surface turbulence
-
- Published online by Cambridge University Press:
- 07 January 2025, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability analysis of a thin liquid film on a horizontal wall under quasi-periodic oscillation
-
- Published online by Cambridge University Press:
- 08 January 2025, A39
-
- Article
- Export citation
Controlled Haines jumps in a dual-channel multiphase system: inferring fluid properties from the dynamics of interface motion
-
- Published online by Cambridge University Press:
- 08 January 2025, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the interaction between planar incident shock with finite width and cylindrical boundary layer at Mach 2.0
-
- Published online by Cambridge University Press:
- 06 February 2025, A41
-
- Article
- Export citation
Mode-to-mode nonlinear energy transfer in turbulent channel flows
-
- Published online by Cambridge University Press:
- 08 January 2025, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition to the buoyancy-dominated regime in a planar temporal forced plume
-
- Published online by Cambridge University Press:
- 14 February 2025, A43
-
- Article
- Export citation
The flow field due to a sphere moving in a viscous, density-stratified fluid
-
- Published online by Cambridge University Press:
- 08 January 2025, A44
-
- Article
- Export citation
Damping of solitons by coastal vegetation
-
- Published online by Cambridge University Press:
- 10 January 2025, A45
-
- Article
- Export citation
Fluttering motion of a confined cylinder falling freely in fluid at rest
-
- Published online by Cambridge University Press:
- 09 January 2025, A46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unsteady flow field behind levitated short-finite circular cylinder with angle of attack
-
- Published online by Cambridge University Press:
- 09 January 2025, A47
-
- Article
- Export citation
Modelling dispersion in stratified turbulent flows as a resetting process
-
- Published online by Cambridge University Press:
- 09 January 2025, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transformation of small-amplitude internal waves passing over a bottom step in a two-layer fluid
-
- Published online by Cambridge University Press:
- 09 January 2025, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Run-out scaling of granular column collapses on inclined planes
-
- Published online by Cambridge University Press:
- 09 January 2025, A50
-
- Article
- Export citation
Turbulent shear flow without vortex shedding, Reynolds shear stress and small-scale intermittency
-
- Published online by Cambridge University Press:
- 09 January 2025, A51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
On wave-driven propulsion – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 09 January 2025, E1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 1002 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 February 2025, p. f1
-
- Article
-
- You have access
- Export citation