This paper is concerned with rapid distortion theory on transversely sheared mean flows that (among other things) can be used to analyse the unsteady motion resulting from the interaction of a turbulent shear flow with a solid surface. It expands on a previous analysis of Goldstein et al. (J. Fluid Mech., vol. 824, 2017, pp. 477–512) that uses a pair of conservation laws to derive upstream boundary conditions for planar mean flows and extends these findings to transversely sheared flows of arbitrary cross-section. The results, which turn out to be quite general, are applied to the specific case of a round jet interacting with the trailing edge of a flat plate and are used to calculate the radiated sound field, which is then compared with experimental data taken at the NASA Glenn Research Center.

Grid is an important factor in numerical simulation of hypersonic aerothermodynamics. This paper introduces three criteria for determining grid size in the transition flow regime when using the computational fluid dynamics (CFD) method or the direct simulation Monte Carlo (DSMC) method. The numerical relationship between these three criteria sizes is deduced according to the one-dimensional fluid theory. Then, the relationship is verified using the CFD method to simulate the flow around a two-dimensional cylinder. At the same time, the dependence of simulation accuracy on grid size in the CFD and DSMC methods is studied and the mechanism is given. The result shows that the simulation accuracy of heat flux especially depends on the normal grid size next to surfaces, where the $Re_{\mathit{cell},w}$ criterion and the $\unicode[STIX]{x1D706}_{w}$ criterion based on local parameters are applicable and equivalent, while the $Re_{\mathit{cell},\infty }$ criterion based on the free-stream parameter is only applicable under the assumption of constant viscosity coefficient and constant temperature wall conditions. On the other hand, the trend of the heat flux changing with grid size obtained by CFD and DSMC is exactly the opposite. Therefore, the grid size must be strictly satisfied with the grid criteria when comparing CFD with DSMC and even the hybrid DSMC with Navier–Stokes method.

We report direct numerical simulation results that clearly elucidate the mechanism that leads to curvature dependence of drag enhancement (DE) in viscoelastic turbulent Taylor–Couette flow. Change in the angular momentum transport and its inherent link to transitions in vortical flow structures have been explored to depict the influence of the curvature of the flow geometry on DE. Specifically, it has been demonstrated that a transition in vortical structures with increasing radius ratio leads to weakening and elimination of the small-scale Görtler vortices and development and better organization (occupying the entire gap) of large-scale Taylor vortices as also evinced by the patterns of angular momentum current. The commensurate change in DE and its underlying mechanism are examined by contributions of convective flux and polymeric stress to the angular momentum current. The present finding paves the way for capturing highly localized elastic turbulence structures in direct numerical simulation by increasing geometry curvature in traditional turbulent curvilinear flows.

The transonic flow field around a supercritical airfoil is investigated. The objective of the present paper is to enhance the understanding of the physical mechanics behind two-dimensional transonic buffet. The paper is composed of two parts. In the first part, a global stability analysis based on the linearized Reynolds-averaged Navier–Stokes equations is performed. A recently developed technique, based on the direct and adjoint unstable global modes, is used to compute the local contribution of the flow to the growth rate and angular frequency of the unstable global mode. The results allow us to identify which zones are directly responsible for the existence of the instability. The technique is firstly used for the vortex-shedding cylinder mode, as a validating case. In the second part, in order to confirm the results of the first part, a selective frequency damping method is locally used in some regions of the flow field. This method consists of applying a low-pass filter on selected zones of the computational domain in order to damp the fluctuations. It allows us to identify which zones are necessary for the persistence of the instability. The two different approaches give the same results: the shock foot is identified as the core of the instability; the shock and the boundary layer downstream of the shock are also necessary zones while damping the fluctuations on the lower surface of the airfoil; and outside the boundary layer between the shock and the trailing edge or above the supersonic zone does not suppress the shock oscillation. A discussion on the several physical models, proposed until now for the buffet phenomenon, and a new model are finally offered in the last section.

We study rotating homogeneous turbulent convection forced by a mean vertical temperature gradient by means of direct numerical simulations in the Boussinesq approximation in a rotating frame. In the absence of rotation, our results are in agreement with the ‘ultimate regime of thermal convection’ for the scaling of the Nusselt and Reynolds numbers versus Rayleigh and Prandtl numbers. Rotation is found to increase both $Nu$ and $Re$ at fixed $Ra$ with a maximum enhancement for intermediate values of the Rossby numbers, qualitatively similar, but with stronger intensity, to what is observed in Rayleigh–Bénard rotating convection. Our results are interpreted in terms of a quasi-bidimensionalization of the flow with the formation of columnar structures displaying strong correlation between the temperature and the vertical velocity fields.

This paper extends a previous study of free-surface flow over two localised obstacles using the framework of the forced Korteweg–de Vries equation, to an analogous study of flow over two localised holes, or a combination of an obstacle and a hole. Importantly the terminology obstacle or hole can be reversed for a stratified fluid and refers more precisely to the relative polarity of the forcing and the solitary wave solution of the unforced Korteweg–de Vries equation. As in the previous study, our main concern is with the transcritical regime when the oncoming flow has a Froude number close to unity. In the transcritical regime at early times, undular bores are produced upstream and downstream of each forcing site. We then describe the interaction of these undular bores between the forcing sites, and the outcome at very large times.

We use direct numerical simulations to investigate the interaction between the temperature field of a fluid and the temperature of small particles suspended in the flow, employing both one- and two-way thermal coupling, in a statistically stationary, isotropic turbulent flow. Using statistical analysis, we investigate this variegated interaction at the different scales of the flow. We find that the variance of the carrier flow temperature gradients decreases as the thermal response time of the suspended particles is increased. The probability density function (PDF) of the carrier flow temperature gradients scales with its variance, while the PDF of the rate of change of the particle temperature, whose variance is associated with the thermal dissipation due to the particles, does not scale in such a self-similar way. The modification of the fluid temperature field due to the particles is examined by computing the particle concentration and particle heat fluxes conditioned on the magnitude of the local fluid temperature gradient. These statistics highlight that the particles cluster on the fluid temperature fronts, and the important role played by the alignments of the particle velocity and the local fluid temperature gradient. The temperature structure functions, which characterize the temperature fluctuations across the scales of the flow, clearly show that the fluctuations of the carrier flow temperature increments are monotonically suppressed in the two-way coupled regime as the particle thermal response time is increased. Thermal caustics dominate the particle temperature increments at small scales, that is, particles that come into contact are likely to have very large differences in their temperatures. This is caused by the non-local thermal dynamics of the particles: the scaling exponents of the inertial particle temperature structure functions in the dissipation range reveal very strong multifractal behaviour. Further insight is provided by the flux of temperature increments across the scales. Altogether, these results reveal a number of non-trivial effects, with a number of important practical consequences.

We present laboratory experiments that show that fingering patterns can emerge when circular interfaces of strain-rate-softening fluids displace less viscous fluids in extensionally dominated flows. The fingers were separated by regions in which the fluid appeared to be torn apart. Initially, the interface had a large dominant wavenumber, but some of the fingers progressively merged so that the number of fingers gradually declined in time. We find that the transition rate to a lower wavenumber during this cascade is faster the larger is the discharge flux of the displacing fluid. At late times, depending on the discharge flux, the pattern either converged into an integer wavenumber or varied stochastically within a finite range of wavenumbers, implying convergence to a fractional wavenumber. In that stage of the evolution we find that the average wavenumber declines with the discharge flux of the displacing fluid.

The interface of a strain-rate-softening fluid that displaces a low-viscosity fluid in a circular geometry with negligible drag can develop finger-like patterns separated by regions in which the fluid appears to be torn apart. Such patterns were observed and explored experimentally in Part 1 using polymeric solutions. They do not occur when the viscosity of the displacing fluid is constant, or when the displacing fluid has no-slip conditions along its boundaries. We investigate theoretically the formation of tongues at the interface of an axisymmetric initial state. We show that finger-like patterns can emerge when circular interfaces of strain-rate-softening fluids displace low-viscosity fluids between stress-free boundaries. The instability, which is fundamentally different from the classical Saffman–Taylor viscous fingering, is driven by the tension that builds up along the circular front of the propagating fluid. That destabilising tension is a geometrical consequence and is present independently of the nonlinear properties of the fluid. Shear stresses stabilise the growth either along extended circumferential streamlines or through a street of vortices. However, such stabilising processes become weaker, thereby allowing the instability to develop, the more strain-rate-softening the fluid is. The theoretical model that we present predicts the main experimental observations made in Part 1. In particular, the patterns we predict using linear-stability theory are consistent with the strongly nonlinear experimental patterns. Our model depends on a single dimensionless number representing the power-law exponent, which implies that the instability we describe could arise in any extensional flow of strain-rate-softening material, ranging from suspensions that rupture in squeeze experiments to rifts formed in ice shelves.

The unsteady flow due to a sphere, immersed in a quiescent fluid, and suddenly rotated, is a paradigm for the development of unsteady boundary layers and their collision. Such a collision arises when the boundary layers on the surface of the sphere are advected towards the equator, where they collide, serving to generate a radial jet. We present the first particle image velocimetry measurements of this collision process, the resulting starting vortex and development of the radial jet. Coupled with new computations, we demonstrate that the post-collision steady flow detaches smoothly from the sphere’s surface, in qualitative agreement with the analysis of Stewartson (Grenzschichtforschung/Boundary Layer Research (ed. H. Görtler), Springer, 1958, pp. 60–70), with no evidence of a recirculation zone, contrary to the conjectured structure of Smith & Duck (Q. J. Mech. Appl. Maths, vol. 20, 1977, pp. 143–156).

In the energy stability theory, the critical Reynolds number is usually defined as the minimum of the first positive eigenvalue $R_{1}$ of an eigenvalue equation for all wavenumber pairs $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$, where $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D6FD}$ are the streamwise and spanwise wavenumbers of the normal mode. We prove that $(\cos \unicode[STIX]{x1D703}\pm 1)R_{1}$ are decreasing functions of $\unicode[STIX]{x1D703}=\arctan (\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D6FC})$ for the parallel flows between no-slip or slip parallel plates with or without variations in temperature. Numerical results inspire us to conjecture that $R_{1}$ is also a decreasing function of $\unicode[STIX]{x1D703}$ for the parallel shear flows under the no-slip boundary condition and without variations in temperature. If the conjecture is correct, the least stable normal modes for the energy stability will be streamwise vortices for these base flows.

Flexible structures placed within an oncoming flow exhibit far more complex vortex-induced dynamics than flexibly mounted rigid cylinders, because they involve the distributed interaction between the structural and wake dynamics along the entire span. Hence, mapping the well-understood properties of rigid cylinder vibrations to those of strings and beams has been elusive. We show here with a combination of experiments, conducted at Reynolds number, 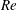$Re$ from 250 to 2300, and computational fluid dynamics that such a mapping is possible for flexible structures in uniform flow undergoing combined cross-flow and in-line oscillations, but only when additional concepts are introduced to model the extended coupling of the flow and the structure. The in-line response consists of largely standing waves that define cells, each cell spanning the distance between adjacent nodes, over which stable vortical patterns form, whose features (‘2S’ versus ‘P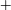$+$S’) depend strongly on the true reduced velocity, 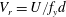$V_{r}=U/f_{y}d$, where 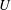$U$ is the inflow velocity, 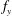$f_{y}$ is the cross-flow vibration frequency and 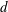$d$ is the cylinder diameter, and the phase angle between in-line and cross-flow response; while the cross-flow response may contain travelling waves, breaking the symmetry of the problem. The axial distribution of the highly variable effective added masses in the cross-flow and in-line directions, and the local phase angle between in-line and cross-flow motion determine the single frequency of cross-flow response, while the in-line response vibrates at twice the cross-flow frequency. The cross-flow and in-line lift coefficients in phase with velocity depend strongly on the true reduced velocity but also on the local phase angle between in-line and cross-flow motions. Modal shapes can be defined for in-line and cross-flow, based on the resemblance of the response to conventional modes, which can be in the ratio of either ‘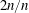$2n/n$’ or ‘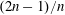$(2n-1)/n$’, where $n$ is the order of the cross-flow response mode. We use an underwater optical tracking system to reconstruct the sectional fluid forces in a flexible structure and show that, once the cross-flow and in-line motion features are known, employing strip theory and the hydrodynamic coefficients obtained from forced rigid cylinder experiments allows us to predict the distributed forces accurately.

We herein report an experimental study to explore the effects of impact inertia, film thickness and viscosity on the dynamics of shape deformation of a drop impacting a liquid film. We have identified that the spreading dynamics shows a weak dependence on impact inertia, but strongly depends on the film thickness. For a thick film, the liquid surface deforms and absorbs part of the impact energy, and hence inhibits spreading of the drop. For a thin film, the drop motion is restricted by the bottom solid substrate, promoting spreading. The periodicity of the capillary controlled shape oscillation, on the other hand, is found to be independent of impact inertia and film thickness. The damping of the shape oscillation shows strong dependence on the film thickness, in that the oscillation decays faster for smaller film thicknesses, due to the enhanced viscous loss.

The dynamics and wall collision of inertial particles were investigated in non-isotropic turbulence of a horizontal liquid channel flow. The inertial particles were $125~\unicode[STIX]{x03BC}\text{m}$ glass beads at a volumetric concentration of 0.03 %. The bead-laden flow and the unladen base case had the same volumetric flow rates, with a shear Reynolds number, $Re_{\unicode[STIX]{x1D70F}}$, of the unladen flow equal to 410 based on the half-channel height and friction velocity. Lagrangian measurements of three-dimensional trajectories of both fluid tracers and glass beads were obtained using time-resolved particle tracking velocimetry based on the shake-the-box algorithm of Schanz et al. (Exp. Fluids, vol. 57, no. 5, 2016, pp. 1–27). The analysis showed that on average the near-wall glass beads decelerate in the streamwise direction, while farther away from the wall, the streamwise acceleration of the glass beads became positive. The ejection motions provided a local maximum streamwise acceleration above the buffer layer by transporting glass beads to high velocity layers and exposing them to a high drag force in the streamwise direction. Conversely, the sweep motion made the maximum contribution to the average streamwise deceleration of glass beads in the near-wall region. The wall-normal acceleration of the beads was positive in the vicinity of the wall, and it became negative farther from the wall. The investigation showed that the glass beads with sweeping motion had the maximum momentum, streamwise deceleration, and wall-normal acceleration among all the beads close to the wall and these values increased with increasing their trajectory angle. The investigation of the beads that collided with the wall showed that those with shallow impact angles (less than $1.5^{\circ }$) typically slide along the wall. The sliding beads had a small streamwise momentum exchange of ${\sim}5\,\%$ during these events. The duration of their sliding motion could be as much as five times the inner time scale of the unladen flow. The wall-normal velocity of these beads after sliding was greater than their wall-normal velocity before sliding, and was associated with the rotation induced lift force. Beads with impact angles greater than $1.5^{\circ }$ had shorter interaction times with the wall and smaller streamwise and wall-normal restitution ratios.

The governing equations of a surface wave field and a coexisting roll–streak circulation typical of Langmuir circulations or submesoscale frontal circulations are derived to better describe their two-way interactions. The gradients and vertical velocities of the roll–streak circulation induce wave refraction, amplitude modulation and higher-order waves. These changes then produce wave–wave nonlinear forces and divergence of the wave-induced mass transport, both of which in turn affect the circulation. To accurately represent these processes, both a wave theory and a wave-averaged theory are developed without relying on any extrapolation, any spatiotemporal mapping or an approximation that treats the wave-induced mass divergence as being concentrated at the surface. This wave theory finds seven types of current-induced higher-order wave motions. It also determines the wave dynamics such as the governing equation of the wave action density valid in the presence of the complex circulation. The evolution of the wave action density is clearly affected by the upwelling or downwelling. The new wave-averaged theory presents the governing equations of the wave-averaged circulation which satisfies the wave-averaged mass conservation. This circulation is different from the circulation considered to satisfy the mass conservation in the Craik–Leibovich theory, and the difference becomes critical when the wave field evolves due to refraction. In this case, compared to the Craik–Leibovich theory, long waves are more important and also the rolls are more weakly forced.

The experimental study on thermocapillary convection in liquid bridges of large Prandtl number has been carried out on Tiangong-2 in space. The purpose of these experiments is to study the oscillation instability of thermocapillary convection, and to discover and recognize the mechanism of destabilization of thermocapillary convection in the microgravity environment in space. In this paper, the geometry of a half-floating-zone liquid bridge is featured by the aspect ratio Ar and volume ratio Vr, and its influence on critical conditions of oscillatory thermocapillary convection is studied. More than 700 sets of space experiments have been finished. The critical conditions and oscillation characteristics of thermocapillary convection instability in the Ar–Vr parameter space have been fully obtained under microgravity conditions for the first time. It is found that the Ar–Vr parameter space can be divided into two regions of different critical conditions and oscillation characteristics: the region of low frequency oscillation, and the region of high frequency oscillation. More importantly, we obtain the complete configuration of these two stability neutral curves, and find that the low frequency mode is a ‘’ type curve. Based on this, we discuss the influence of heating rate on the oscillation mode. It is found that the heating rate affects the selection of critical mode, which results in a jump change of critical temperature difference. The findings of this study are helpful to better understand the critical modes and transition processes of thermocapillary convection in liquid bridges with different configurations.

Rectilinear collisions of three wetted spheres are considered under conditions of high capillary numbers, for which viscous lubrication forces dominate over capillary forces. The viscous forces resist the relative motion, as characterized by the Stokes number (a dimensionless ratio of particle inertia and viscous forces). At high Stokes numbers, the particles penetrate the fluid layers between them with sufficient inertia that they collide and rebound. Both simultaneous and sequential collisions are simulated, and various outcomes are demonstrated: full agglomeration of the three spheres at low Stokes numbers, full separation or Newton’s cradle at large Stokes numbers and even reverse Newton’s cradle at intermediate Stokes numbers when there is a thicker combined fluid layer between the two target spheres than between the striker sphere and the first target sphere. When there is an initial air gap between the two target spheres, even more exotic outcomes are predicted, such as full separation after the initial collisions followed by full agglomeration or reverse Newton’s cradle (intermediate Stokes numbers) or Newton’s cradle (large Stokes numbers) after the subsequent collisions when the striker sphere catches back up to the target spheres. The approach and findings of this work are expected to provide input and guidance to future work on discrete-element modelling of collisions of many wet particles.

We examine the origin of very-large-scale motions (VLSMs) in fully developed turbulent pipe flow at friction Reynolds number, $\mathit{Re}_{\unicode[STIX]{x1D70F}}=934$, using data from a direct numerical simulation. The VLSMs and the packet-like large-scale motions (LSMs) found in this study are very similar to those found in earlier studies. Three-dimensional time-evolving instantaneous fields show that one component of the process leading to the large streamwise length of VLSMs is the concatenation of adjacent streamwise LSMs caused by the continuous elongation of LSMs due to the strain component of the mean shear. Spatial organization patterns of the VLSMs and LSMs and their properties are studied by separating auto-correlation of the streamwise velocity fluctuations into the components of the VLSM and the LSM defined by low-pass/high-pass filtering in the streamwise direction. The structures of the two-point spatial correlations of the streamwise velocity component of the VLSMs and the LSMs in the streamwise-azimuthal plane are characterized by multiple maxima and complex patterns that beg explanation in terms of patterned coherent arrangements of the LSMs. Using proper orthogonal decomposition (POD), it is found that the X-shape correlation pattern of the VLSMs results from the superposition of very long helically inclined structures and streamwise-aligned structures. Further explanation of the patterns in the correlations of the VLSMs and LSMs is provided through the study of synthetically constructed arrangements of simple hairpin packet models of the LSM. Head-to-tail alignment of the model packets along streamwise and helical directions suggested by the eigenvalues of the POD creates a pair of long roll-cells centred above the logarithmic layer, and bracketing the LSMs. These roll-cells are pure kinematic consequences of the induction within the LSM packets, but they may also serve to organize smaller packets.

This work analyses the viscous flow and elastic deformation created by the forced axial motion of a rigid cylinder within an elastic liquid-filled tube. The examined configuration is relevant to various minimally invasive medical procedures in which slender devices are inserted into fluid-filled biological vessels, such as vascular interventions, interventional radiology, endoscopies and laparoscopies. By applying the lubrication approximation, thin shell elastic model, as well as scaling analysis and regular and singular asymptotic schemes, the problem is examined for small and large deformation limits (relative to the gap between the cylinder and the tube). At the limit of large deformations, forced insertion of the cylinder is shown to involve three distinct regimes and time scales: (i) initial shear dominant regime, (ii) intermediate regime of dominant fluidic pressure and a propagating viscous-peeling front, (iii) late-time quasi-steady flow regime of the fully peeled tube. A uniform solution for all regimes is presented for a suddenly applied constant force, showing initial deceleration and then acceleration of the inserted cylinder. For the case of forced extraction of the cylinder from the tube, the negative gauge pressure reduces the gap between the cylinder and the tube, increasing viscous resistance or creating friction due to contact of the tube and cylinder. Matched asymptotic schemes are used to calculate the dynamics of the near-contact and contact limits. We find that the cylinder exits the tube in a finite time for sufficiently small or large forces. However, for an intermediate range of forces, the radial contact creates a steady locking of the cylinder inside the tube.

Rayleigh–Bénard convection in water is studied by means of direct numerical simulations, taking into account the variation of properties. The simulations considered a three-dimensional (3-D) cavity with a square cross-section and its two-dimensional (2-D) equivalent, covering a Rayleigh number range of $10^{6}\leqslant Ra\leqslant 10^{9}$ and using temperature differences up to 60 K. The main objectives of this study are (i) to investigate and report differences obtained by 2-D and 3-D simulations and (ii) to provide a first appreciation of the non-Oberbeck–Boussinesq (NOB) effects on the near-wall time-averaged and root-mean-squared (r.m.s.) temperature fields. The Nusselt number and the thermal boundary layer thickness exhibit the most pronounced differences when calculated in two dimensions and three dimensions, even though the $Ra$ scaling exponents are similar. These differences are closely related to the modification of the large-scale circulation pattern and become less pronounced when the NOB values are normalised with the respective Oberbeck–Boussinesq (OB) values. It is also demonstrated that NOB effects modify the near-wall temperature statistics, promoting the breaking of the top–bottom symmetry which characterises the OB approximation. The most prominent NOB effect in the near-wall region is the modification of the maximum r.m.s. values of temperature, which are found to increase at the top and decrease at the bottom of the cavity.