The phenomenon of lock-in in vortex-induced vibration of a circular cylinder is
investigated in the laminar flow regime (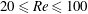 $20\leqslant Re\leqslant 100$). Direct time integration (DTI) and linear stability analysis (LSA)
of the governing equations are carried out via a stabilized finite element method.
Using the metrics that have been proposed in earlier studies, the lock-in regime is
identified from the results of DTI. The LSA yields the eigenmodes of the coupled
fluid–structure system, the associated frequencies (
$20\leqslant Re\leqslant 100$). Direct time integration (DTI) and linear stability analysis (LSA)
of the governing equations are carried out via a stabilized finite element method.
Using the metrics that have been proposed in earlier studies, the lock-in regime is
identified from the results of DTI. The LSA yields the eigenmodes of the coupled
fluid–structure system, the associated frequencies (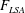 $F_{LSA}$) and the stability of the steady state. A linearly unstable system,
in the absence of nonlinear effects, achieves large oscillation amplitude at
sufficiently large times. However, the nonlinear terms saturate the response of the
system to a limit cycle. For subcritical
$F_{LSA}$) and the stability of the steady state. A linearly unstable system,
in the absence of nonlinear effects, achieves large oscillation amplitude at
sufficiently large times. However, the nonlinear terms saturate the response of the
system to a limit cycle. For subcritical 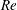 $Re$, the occurrence of lock-in coincides with the linear instability of
the fluid–structure system. The critical
$Re$, the occurrence of lock-in coincides with the linear instability of
the fluid–structure system. The critical 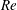 $Re$ is the Reynolds number beyond which vortex shedding ensues for a
stationary cylinder. For supercritical
$Re$ is the Reynolds number beyond which vortex shedding ensues for a
stationary cylinder. For supercritical 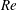 $Re$, even though the aeroelastic system is unstable for all reduced
velocities (
$Re$, even though the aeroelastic system is unstable for all reduced
velocities (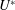 $U^{\ast }$) lock-in occurs only for a finite range of
$U^{\ast }$) lock-in occurs only for a finite range of 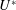 $U^{\ast }$. We present a method to estimate the time beyond which the
nonlinear effects are expected to be significant. It is observed that much of the
growth in the amplitude of cylinder oscillation takes place in the linear regime. The
response of the cylinder at the end of the linear regime is found to depend on the
energy ratio,
$U^{\ast }$. We present a method to estimate the time beyond which the
nonlinear effects are expected to be significant. It is observed that much of the
growth in the amplitude of cylinder oscillation takes place in the linear regime. The
response of the cylinder at the end of the linear regime is found to depend on the
energy ratio, 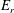 $E_{r}$, of the unstable eigenmode.
$E_{r}$, of the unstable eigenmode. 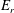 $E_{r}$ is defined as the fraction of the total energy of the eigenmode
that is associated with the kinetic and potential energy of the structure. DTI
initiated from eigenmodes that are linearly unstable and whose energy ratio is above
a certain threshold value lead to lock-in. Interestingly, during lock-in, the
oscillation frequency of the fluid–structure system drifts from
$E_{r}$ is defined as the fraction of the total energy of the eigenmode
that is associated with the kinetic and potential energy of the structure. DTI
initiated from eigenmodes that are linearly unstable and whose energy ratio is above
a certain threshold value lead to lock-in. Interestingly, during lock-in, the
oscillation frequency of the fluid–structure system drifts from 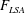 $F_{LSA}$ towards a value that is closer to the natural frequency of the
oscillator in vacuum (
$F_{LSA}$ towards a value that is closer to the natural frequency of the
oscillator in vacuum (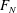 $F_{N}$). In the event of more than one eigenmode being linearly unstable,
we investigate which one is responsible for lock-in. The concept of phase angle
between the cylinder displacement and lift is extended for an eigenmode. The phase
angle controls the direction of energy transfer between the fluid and the structure.
For zero structural damping, if the phase angle of all unstable eigenmodes is less
than 90°, the phase angle obtained via DTI evolves to a value that is
close to 0°. If, on the other hand, the phase angle of any unstable
eigenmode is more than 90°, it settles to 180°, approximately
in the limit cycle. A new approach towards classification of modes is presented. The
eigenvalues are tracked over a wide range of
$F_{N}$). In the event of more than one eigenmode being linearly unstable,
we investigate which one is responsible for lock-in. The concept of phase angle
between the cylinder displacement and lift is extended for an eigenmode. The phase
angle controls the direction of energy transfer between the fluid and the structure.
For zero structural damping, if the phase angle of all unstable eigenmodes is less
than 90°, the phase angle obtained via DTI evolves to a value that is
close to 0°. If, on the other hand, the phase angle of any unstable
eigenmode is more than 90°, it settles to 180°, approximately
in the limit cycle. A new approach towards classification of modes is presented. The
eigenvalues are tracked over a wide range of 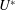 $U^{\ast }$ while keeping
$U^{\ast }$ while keeping 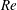 $Re$ and mass ratio (
$Re$ and mass ratio (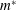 $m^{\ast }$) fixed. In general, for large values of
$m^{\ast }$) fixed. In general, for large values of 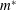 $m^{\ast }$, the eigenmodes corresponding to the two leading eigenvalues
exhibit a decoupled behaviour with respect to
$m^{\ast }$, the eigenmodes corresponding to the two leading eigenvalues
exhibit a decoupled behaviour with respect to 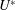 $U^{\ast }$. They are classified as the fluid and elastic modes. However, for
relatively low
$U^{\ast }$. They are classified as the fluid and elastic modes. However, for
relatively low 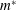 $m^{\ast }$ such a classification is not possible. The two leading modes are
coupled and are referred to as fluid–elastic modes. The regime of such
occurrence is shown on the
$m^{\ast }$ such a classification is not possible. The two leading modes are
coupled and are referred to as fluid–elastic modes. The regime of such
occurrence is shown on the 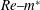 $Re{-}m^{\ast }$ parameter space.
$Re{-}m^{\ast }$ parameter space.