We report an experimental analysis of path and shape oscillations of an air bubble of diameter rising in water at high Reynolds number in a vertical Hele-Shaw cell of width . Liquid velocity perturbations induced by the relative movement have also been investigated to analyse the coupling between the bubble motion and the wake dynamics. The confinement ratio is less than unity so that the bubble is flattened between the walls of the cell. As the bubble diameter is increased, the Archimedes and the Bond numbers increase within the ranges and . Mean shapes become more and more elongated. They first evolve from in-plane circles to ellipses, then to complicated shapes without fore–aft symmetry and finally to semi-circular-capped bubbles. The scaling law is valid for a large range of , however, indicating that the liquid films between the bubble and the walls do not contribute significantly to the drag force exerted on the bubble. The coupling between wake dynamics, bubble path and shape oscillations evolves and a succession of different regimes of oscillations is observed. The rectilinear bubble motion becomes unstable from a critical value through an Hopf bifurcation while the bubble shape is still circular. The amplitude of path oscillations first grows as increases above but then surprisingly decreases beyond a second Archimedes number . This phenomenon, observed for steady ellipsoidal shape with moderate eccentricity, can be explained by the rapid attenuation of bubble wakes caused by the confinement. Shape oscillations around a significantly elongated mean shape start for . The wake structure progressively evolves due to changes in the bubble shape. After the break-up of the fore–aft symmetry, a fourth regime involving complicated shape oscillations is then observed for . Vortex shedding disappears and unsteady attached vortices coupled to shape oscillations trigger path oscillations of moderate amplitude. Path and shape oscillations finally decrease when is further increased. For , capped bubbles followed by a steady wake rise on a straight path.

We examine the oscillatory motion of fluid which spreads under gravity along a horizontal impermeable boundary through a porous medium controlled by the periodic injection and extraction of fluid from a horizontal well. Over the first few cycles the volume of injected fluid exceeds that which is extracted owing to the gravitational spreading of the current. However, after many cycles, these volumes converge and the flow develops into two regions. Near the source there is a zone 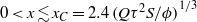in which the depth of the fluid varies periodically with each cycle, where 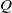is the fluid injection rate, is the injection or extraction time, 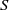is the speed of the buoyancy-driven flow and 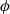is the porosity. The current attains its maximum depth, 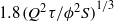at the source, where the minimum depth equals zero. At long times, the current depth at 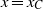is approximately constant, 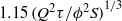, and beyond this point, the current spreads horizontally, driven by an effective flux 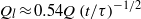, so that the length of the current increases as 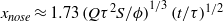. We confirm these predictions with new experiments using a Hele-Shaw cell. We also model the evolution of the thermal front which develops if the injected fluid is hotter than the formation temperature. We find conditions under which all the extracted fluid is hot but owing to the mismatch between the volume of injected and extracted fluids, not all the injected thermal energy is recovered, and the surrounding rock heats up.

The classical Schlichting boundary layer theory is extended to account for the excitation of generalized surface waves in the frequency and velocity amplitude range commonly used in microfluidic applications, including Rayleigh and Sezawa surface waves and Lamb, flexural and surface-skimming bulk waves. These waves possess longitudinal and transverse displacements of similar magnitude along the boundary, often spatiotemporally out of phase, giving rise to a periodic flow shown to consist of a superposition of classical Schlichting streaming and uniaxial flow that have no net influence on the flow over a long period of time. Correcting the velocity field for weak but significant inertial effects results in a non-vanishing steady component, a drift flow, itself sensitive to both the amplitude and phase (prograde or retrograde) of the surface acoustic wave propagating along the boundary. We validate the proposed theory with experimental observations of colloidal pattern assembly in microchannels filled with dilute particle suspensions to show the complexity of the boundary layer, and suggest an asymptotic slip boundary condition for bulk flow in microfluidic applications that are actuated by surface waves.

Dynamic wetting is crucial to processes where liquid displaces another fluid along a solid surface, such as the deposition of a coating liquid onto a moving substrate. Numerous studies report the failure of dynamic wetting past some critical process speed. However, the hydrodynamic factors that influence the transition to wetting failure remain poorly understood from an empirical and theoretical perspective. The objective of this investigation is to determine the effect of meniscus confinement on the onset of dynamic wetting failure. A novel experimental system is designed to simultaneously view confined and unconfined wetting systems as they approach wetting failure. The experimental apparatus consists of a scraped steel roll that rotates into a bath of glycerol. Confinement is imposed via a gap formed between a coating die and the roll surface. Flow visualization is used to record the critical roll speed at which wetting failure occurs. Comparison of the confined and unconfined data shows a clear increase in the relative critical speed as the meniscus becomes more confined. A hydrodynamic model for wetting failure is developed and analysed with (i) lubrication theory and (ii) a two-dimensional finite-element method (FEM). Both approaches do a remarkable job of matching the observed confinement trend, but only the two-dimensional model yields accurate estimates of the absolute values of the critical speeds due to the highly two-dimensional nature of the stress field in the displacing liquid. The overall success of the hydrodynamic model suggests a wetting failure mechanism primarily related to viscous bending of the meniscus.

Liquid bridges with moving contact lines are relevant in a variety of natural and industrial settings, ranging from printing processes to the feeding of birds. While it is often assumed that the liquid bridge is two-dimensional in nature, there are many applications where either the stretching motion or the presence of a feature on a bounding surface lead to three-dimensional effects. To investigate this we solve Stokes equations using the finite-element method for the stretching of a three-dimensional liquid bridge between two flat surfaces, one stationary and one moving. We first consider an initially cylindrical liquid bridge that is stretched using either a combination of extension and shear or extension and rotation, while keeping the contact lines pinned in place. We find that whereas a shearing motion does not alter the distribution of liquid between the two plates, rotation leads to an increase in the amount of liquid resting on the stationary plate as breakup is approached. This suggests that a relative rotation of one surface can be used to improve liquid transfer to the other surface. We then consider the extension of non-cylindrical bridges with moving contact lines. We find that dynamic wetting, characterized through a contact line friction parameter, plays a key role in preventing the contact line from deviating significantly from its original shape as breakup is approached. By adjusting the friction on both plates it is possible to drastically improve the amount of liquid transferred to one surface while maintaining the fidelity of the liquid pattern.

The three-dimensional structure of the leading-edge vortex on a rotating wing is addressed using a technique of particle image velocimetry. Organized patterns of chordwise-oriented vorticity, which exist within the vortex, arise from the spanwise flow along the surface of the wing, which can attain a velocity the same order as the velocity of the wing at its radius of gyration. These patterns are related to the strength (circulation) and coherence of the tip and root vortices. The associated distributions of spanwise-oriented vorticity along the leading-edge vortex are characterized in relation to the vorticity flux and downwash along the wing.

Experimental data are presented for the vortex flow in a nominally two-dimensional circular cavity. The vortex is driven by a separated shear layer along an open section of the cavity circumference. It is shown that the core vortex flow is perturbed three-dimensionally. An inviscid analysis of an ideal core (solid body) vortex is given and it is shown that this flow contains a steady perturbation whose characteristics are almost exactly those identified in the experiments. Viscous effects reduce (by a few per cent) the spanwise wavelength of the perturbation and also lead, via spatial variations in Reynolds stress, to a modification of the core flow so that the radial profile of the circumferential velocity is ‘S’-shaped, rather than linear.

A new theory for the streamwise turbulent fluctuations in fully developed pipe flow is proposed. The theory extends the similarities between the mean flow and the streamwise turbulence fluctuations, as observed in experimental high Reynolds number data, to also include the theoretical derivation. Connecting the derivation of the fluctuations to that of the mean velocity at finite Reynolds number as introduced by Wosnik, Castillo & George (J. Fluid Mech., vol. 421, 2000, pp. 115–145) can explain the logarithmic behaviour as well as the coefficient of the logarithm. The slope of the logarithm, for the fluctuations, depends on the increase of the fluctuations with Reynolds number, which is shown to agree very well with the experimental data. A mesolayer, similar to that introduced by Wosnik et al., exists for the fluctuations for , which coincides with the mesolayer for the mean velocities. In the mesolayer, the flow is still affected by viscosity, which shows up as a decrease in the fluctuations.

We obtain the fully nonlinear local induction equation describing the motion of a vortex filament in superfluid 4He. As the relevant friction parameters are small, we linearize terms involving such parameters, while keeping the remaining nonlinearities, which accurately describe the curvature of the vortex filament, intact. The resulting equation is a type of nonlinear Schrödinger equation, and, under an appropriate change of variables, this equation is shown to have a first integral. This is in direct analogy with the simpler equation studied previously in the literature; indeed, in the limit where the superfluid parameters are taken to zero, we recover the results of Van Gorder. While this first integral is mathematically interesting, it is not particularly useful for computing solutions to the nonlinear partial differential equation which governs the vortex filament. As such, we introduce a new change of dependent variable, which results in a nonlinear four-dimensional system that can be numerically integrated. Integrating this system, we recover solutions to the fully nonlinear local induction equation describing the motion of a vortex filament in superfluid 4He. We find that the qualitative features of the solutions depend not only on the superfluid friction parameters, but also strongly on the initial conditions taken, the curvature and the normal fluid velocity.

We analyse the disturbed flow in the subsonic laminar boundary layer, disturbances being generated by local heating elements, which are placed on the surface. It is exhibited that these flows are described in terms of free interaction theory for specific sizes of thermal sources. We construct the numerical solution for the case of a flat subsonic stream in the viscous asymptotic layer, in which the flow is described by nonlinear equations for vorticity, temperature and an interaction condition which provides the influence of perturbations to the pressure in the main order. The obtained solutions are compared with those for corresponding linear problems with small perturbations. It is demonstrated that strong temperature perturbations in some situations allow us to obtain the flow close to the separated flow.