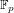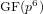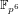Contents
Research Article
Analysis of semilocal convergence for ameliorated super-Halley methods with less computation for inversion
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2016, pp. 293-302
-
- Article
-
- You have access
- Export citation
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
Character theory approach to Sato–Tate groups
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 301-314
-
- Article
-
- You have access
- Export citation
Reducing number field defining polynomials: an application to class group computations
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 315-331
-
- Article
-
- You have access
- Export citation
Collecting relations for the number field sieve in
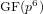 $\text{GF}(p^{6})$
$\text{GF}(p^{6})$
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 332-350
-
- Article
-
- You have access
- Export citation
Databases of elliptic curves ordered by height and distributions of Selmer groups and ranks
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 351-370
-
- Article
-
- You have access
- Export citation
Fast heuristic algorithms for computing relations in the class group of a quadratic order, with applications to isogeny evaluation
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 371-390
-
- Article
-
- You have access
- Export citation
Computing canonical heights on elliptic curves in quasi-linear time
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 391-405
-
- Article
-
- You have access
- Export citation