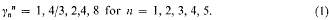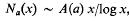Contents
Research Article
On the classgroup of integral grouprings of finite abelian groups
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-152
-
- Article
- Export citation
Respectability of the graphs of composites
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-157
-
- Article
- Export citation
Hankel determinants and meromorphic functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 158-166
-
- Article
- Export citation
Analytic continuation of power series whose coefficients belong to an algebraic number field
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-169
-
- Article
- Export citation
On the minimal points of perfect septenary quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-177
-
- Article
- Export citation
An average result for Artin's conjecture
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-188
-
- Article
- Export citation
The large sieve in algebraic number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-204
-
- Article
- Export citation
Response of a viscoelastic beam to an impulsive excitation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-208
-
- Article
- Export citation
Generation of acoustic pulses by baffled plane pistons
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-224
-
- Article
- Export citation
Eigenfunctions for the symmetrical deformations of a cylinder whose plane faces are stress-free
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-230
-
- Article
- Export citation
Slow time-dependent motion of a hemisphere in a stratified fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-248
-
- Article
- Export citation
Steady magnetohydrodynamic flow in an insulating circular pipe
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 249-262
-
- Article
- Export citation
Triangle models and relations between them
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 263-272
-
- Article
- Export citation
Neighbourliness and Radon's theorem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-275
-
- Article
- Export citation
Characterization of certain polytopes by intersection properties of their translates
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 276-282
-
- Article
- Export citation
Weber's class invariants
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 283-294
-
- Article
- Export citation
On the steady rotation of an axisymmetric solid in a conducting fluid at high Hartmann numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-304
-
- Article
- Export citation
A note on ‘Strong cylindrical shock waves in magnetogasdynamics’
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 305
-
- Article
- Export citation
Corrigendum
Corrigendum: Mathematika Volume 15, 1968
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 306
-
- Article
-
- You have access
- Export citation
Corrigendum: Mathematika Volume 16, 1969
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 307
-
- Article
-
- You have access
- Export citation
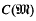 of the maximal order
of the maximal order 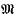 in the rational groupring Q(Γ). Now
in the rational groupring Q(Γ). Now 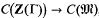 , and it is this which concerns us here. I shall show that it can become very big.
, and it is this which concerns us here. I shall show that it can become very big.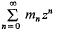 has rational integer coefficients, positive radius of convergence, and can be continued analytically to a region that contains points outside the closed unit disc, then the function that the power series represents is rational. This result has been extended in a number of ways (
has rational integer coefficients, positive radius of convergence, and can be continued analytically to a region that contains points outside the closed unit disc, then the function that the power series represents is rational. This result has been extended in a number of ways (