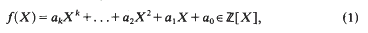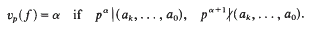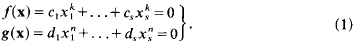Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 12
Planar maps with prescribed types of vertices and faces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 28-36
-
- Article
- Export citation
- Cited by 12
SHAPES OF POLYHEDRA, MIXED VOLUMES AND HYPERBOLIC GEOMETRY
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2016, pp. 124-183
-
- Article
- Export citation
- Cited by 12
On the distribution of apk modulo one
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 170-184
-
- Article
- Export citation
- Cited by 12
OPERATOR ALGEBRAIC APPROACH TO INVERSE AND STABILITY THEOREMS FOR AMENABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2018, pp. 98-118
-
- Article
- Export citation
- Cited by 11
Simple one-point extensions of tournaments
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-62
-
- Article
- Export citation
- Cited by 11
A lattice problem in the plane
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-252
-
- Article
- Export citation
- Cited by 11
The simplified quasigeostrophic equations: Existence and uniqueness of strong solutions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-311
-
- Article
- Export citation
- Cited by 11
ON MULTIPLICATIVELY BADLY APPROXIMABLE NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 June 2012, pp. 31-55
-
- Article
- Export citation
- Cited by 11
POINT DISTRIBUTIONS IN COMPACT METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1152-1171
-
- Article
- Export citation
- Cited by 11
Vortices, Liouville's equation and the Bergman kernel function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 321-334
-
- Article
- Export citation
- Cited by 11
On Hua's estimates for exponential sums
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-123
-
- Article
- Export citation
- Cited by 11
On converging solid spheres in a highly viscous fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 250-254
-
- Article
- Export citation
- Cited by 11
PERMUTATION CLASSES OF EVERY GROWTH RATE ABOVE 2.48188
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 182-192
-
- Article
- Export citation
- Cited by 11
On Cesaro summable sequences of continuous functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-104
-
- Article
- Export citation
- Cited by 11
The two-ball property: transitivity and examples
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 190-197
-
- Article
- Export citation
- Cited by 11
The reduction number of a one-dimensional local ring
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-90
-
- Article
- Export citation
- Cited by 11
The number of plane trees with a given partition
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
-
- Article
- Export citation
- Cited by 11
K-analytic sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-221
-
- Article
- Export citation
- Cited by 11
Products on spheres
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
-
- Article
- Export citation
- Cited by 11
On simultaneous additive equations, III
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-96
-
- Article
- Export citation
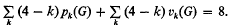
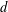
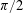
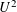
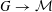
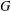
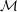

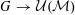

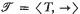 is a relational structure on the non-empty set
is a relational structure on the non-empty set 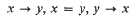
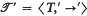 is a
is a 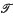 , and
, and 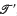 , if
, if 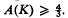 . We prove here a result in the opposite direction.
. We prove here a result in the opposite direction.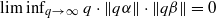 for all (
for all (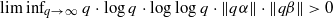 is of full dimension.
is of full dimension.