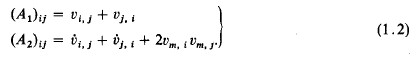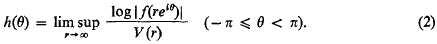Contents
Research Article
Asymptotic formulas for the number of self-complementary graphs and digraphs
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-90
-
- Article
- Export citation
Note on parametrisations of normal elliptic scrolls
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-292
-
- Article
- Export citation
Existence theorem for infinite integral matrices
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-97
-
- Article
- Export citation
Paths in the one-skeleton of a convex body
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 293-314
-
- Article
- Export citation
Reuleaux polytopes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 315-323
-
- Article
- Export citation
Solution of some boundary value problems in potential theory
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-101
-
- Article
- Export citation
The critical layer in stratified shear flow
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-119
-
- Article
- Export citation
Generalized Hausdorff dimension
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 324-327
-
- Article
- Export citation
The distribution of rational points on hypersurfaces defined over a finite field
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 328-332
-
- Article
- Export citation
The number of d-polytopes with d+3 vertices
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 120-132
-
- Article
- Export citation
On uniqueness of flows for a class of second-order fluids
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 333-337
-
- Article
- Export citation
A linear set of infinite measure with no two points having integral ratio
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-138
-
- Article
- Export citation
Index
Index to volume 17
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 338
-
- Article
- Export citation
Research Article
Quotient overrings of integral domains
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-148
-
- Article
- Export citation
A local form of the Phragmén-lindelöf indicator
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-172
-
- Article
- Export citation
Front matter
MTK volume 17 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Corrigendum and addendum: an analogue of a problem of Littlewood
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 173-178
-
- Article
- Export citation
Front matter
MTK volume 17 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
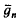 of self-complementary graphs and the number
of self-complementary graphs and the number 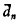 of self-complementary digraphs were expressed by Read [4] in terms of cycle indexes of the appropriate pair groups. These formulas for
of self-complementary digraphs were expressed by Read [4] in terms of cycle indexes of the appropriate pair groups. These formulas for