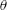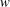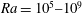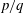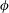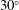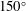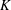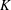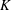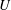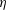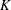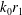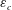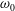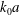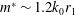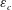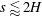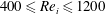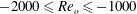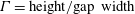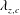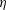JFM Rapids
On the mixing length eddies and logarithmic mean velocity profile in wall turbulence
-
- Published online by Cambridge University Press:
- 21 January 2020, R1
-
- Article
- Export citation
JFM Papers
Gradient diffusion in dilute suspensions of hard spheroidal particles
-
- Published online by Cambridge University Press:
- 17 January 2020, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coherence of temperature and velocity superstructures in turbulent Rayleigh–Bénard flow
-
- Published online by Cambridge University Press:
- 17 January 2020, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental evidence of amplitude modulation in permeable-wall turbulence
-
- Published online by Cambridge University Press:
- 17 January 2020, A3
-
- Article
- Export citation
Numerical analysis of the mean structure of gaseous detonation with dilute water spray
-
- Published online by Cambridge University Press:
- 17 January 2020, A4
-
- Article
- Export citation
Transition to chaos through period doublings of a forced oscillating cylinder in steady current
-
- Published online by Cambridge University Press:
- 21 January 2020, A5
-
- Article
- Export citation
Precessing cube: resonant excitation of modes and triadic resonance
-
- Published online by Cambridge University Press:
- 21 January 2020, A6
-
- Article
- Export citation
Effect of trailing-edge shape on the self-propulsive performance of heaving flexible plates
-
- Published online by Cambridge University Press:
- 21 January 2020, A7
-
- Article
- Export citation
Interaction between an inclined gravity current and a pycnocline in a two-layer stratification
-
- Published online by Cambridge University Press:
- 21 January 2020, A8
-
- Article
- Export citation
Burnett-order constitutive relations, second moment anisotropy and co-existing states in sheared dense gas–solid suspensions
-
- Published online by Cambridge University Press:
- 21 January 2020, A9
-
- Article
- Export citation
Observations of mean and wave orbital flows in the ocean’s upper centimetres
-
- Published online by Cambridge University Press:
- 23 January 2020, A10
-
- Article
- Export citation
Modelling of the turbulent burning velocity based on Lagrangian statistics of propagating surfaces
-
- Published online by Cambridge University Press:
- 23 January 2020, A11
-
- Article
- Export citation
Shock interactions in two-dimensional steady flows of Bethe–Zel’dovich–Thompson fluids
-
- Published online by Cambridge University Press:
- 23 January 2020, A12
-
- Article
- Export citation
Unsteady solute dispersion by electrokinetic flow in a polyelectrolyte layer-grafted rectangular microchannel with wall absorption
-
- Published online by Cambridge University Press:
- 23 January 2020, A13
-
- Article
- Export citation
Excitation of interfacial waves via surface–interfacial wave interactions
-
- Published online by Cambridge University Press:
- 23 January 2020, A14
-
- Article
- Export citation
Compressibility and variable inertia effects on heat transfer in turbulent impinging jets
-
- Published online by Cambridge University Press:
- 28 January 2020, A15
-
- Article
- Export citation
Instability of finite-amplitude gravity–capillary progressive ring waves by an oscillating surface-piercing body
-
- Published online by Cambridge University Press:
- 28 January 2020, A16
-
- Article
- Export citation
Secondary currents and very-large-scale motions in open-channel flow over streamwise ridges
-
- Published online by Cambridge University Press:
- 28 January 2020, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulations of spiral Taylor–Couette turbulence
-
- Published online by Cambridge University Press:
- 28 January 2020, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-similar breakup of polymeric threads as described by the Oldroyd-B model
-
- Published online by Cambridge University Press:
- 28 January 2020, A19
-
- Article
- Export citation