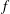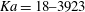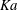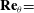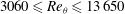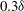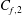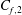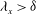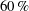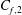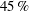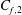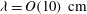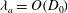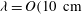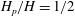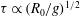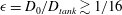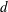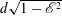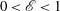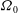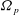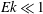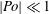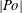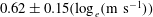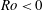Papers
Inertial versus baroclinic instability of the Bickley jet in continuously stratified rotating fluid
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 1-31
-
- Article
- Export citation
Lattice Boltzmann approach to simulating a wetting–drying front in shallow flows
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 32-59
-
- Article
- Export citation
Effects of the particle deformability on the critical separation diameter in the deterministic lateral displacement device
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 60-74
-
- Article
- Export citation
Three-dimensional flow structures in laminar falling liquid films
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 75-123
-
- Article
- Export citation
Mixing and transport by ciliary carpets: a numerical study
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 124-140
-
- Article
- Export citation
On Langmuir circulation in shallow waters
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 141-169
-
- Article
- Export citation
Computational modelling of flow through prosthetic heart valves using the entropic lattice-Boltzmann method
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 170-201
-
- Article
- Export citation
Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to
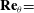 $\mathbf{Re}_{\boldsymbol{\theta}}{=}$13650
$\mathbf{Re}_{\boldsymbol{\theta}}{=}$13650
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 202-248
-
- Article
- Export citation
Vorticity transport in the leading-edge vortex on a rotating blade
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 249-261
-
- Article
- Export citation
Pearling instability of a cylindrical vesicle
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 262-279
-
- Article
- Export citation
Damping of inertial motions by parametric subharmonic instability in baroclinic currents
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 280-294
-
- Article
- Export citation
Water entry without surface seal: extended cavity formation
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 295-326
-
- Article
- Export citation
Viscid–inviscid pseudo-resonance in streamwise corner flow
-
- Published online by Cambridge University Press:
- 04 March 2014, pp. 327-357
-
- Article
- Export citation
On precessing flow in an oblate spheroid of arbitrary eccentricity
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. 358-384
-
- Article
- Export citation
Chaotic rotation of a towed elliptical cylinder
-
- Published online by Cambridge University Press:
- 06 March 2014, pp. 385-398
-
- Article
- Export citation
On the microphysical behaviour of wind-forced water surfaces and consequent re-aeration
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. 399-447
-
- Article
- Export citation
Effective conditions for the reflection of an acoustic wave by low-porosity perforated plates
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. 448-480
-
- Article
- Export citation
Simply-connected vortex-patch shallow-water quasi-equilibria
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. 481-502
-
- Article
- Export citation
Mean structure of one-dimensional unstable detonations with friction
-
- Published online by Cambridge University Press:
- 06 March 2014, pp. 503-533
-
- Article
- Export citation
Topological selection in stratified fluids: an example from air–water systems
-
- Published online by Cambridge University Press:
- 06 March 2014, pp. 534-553
-
- Article
- Export citation