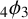 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
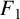 $F_1$
$F_1$
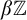 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
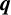 $\boldsymbol {q}$
-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$
-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
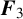 $\boldsymbol F_3$
$\boldsymbol F_3$
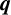 $\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
 $\mathbf {2}$
$\mathbf {2}$