 $2$ CURVE
$2$ CURVE
 ${\mathbb Q}$
${\mathbb Q}$
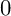 $0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE